
分析 (1)由题意可知圆心M的轨迹为以(0,1)为焦点,直线y=-1为准线的抛物线,根据抛物线的方程即可求得圆心M的轨迹方程;
(2)由题意可知直线l的斜率存在,设直线l的方程为:y=kx-2,A(x1,y1),B(x2,y2),则C(-x2,y2).代入抛物线方,由韦达定理及直线直线AC的方程为:y-y2=-$\frac{{y}_{2}-{y}_{1}}{{x}_{2}+{x}_{1}}$(x+x2),把根与系数的关系代入可得4y=(x2-x1)x+8,令x=0,即可得出直线恒过定点.
解答 解:(1)∵动点M到直线y=-1的距离等于到定点C(0,1)的距离,
∴动点M的轨迹为抛物线,且$\frac{p}{2}$=1,解得:p=2,
∴动点M的轨迹方程为x2=4y;
(2)证明:由题意可知直线l的斜率存在,
设直线l的方程为:y=kx-2,A(x1,y1),B(x2,y2),则C(-x2,y2).
联立$\left\{\begin{array}{l}{y=kx-2}\\{{x}^{2}=4y}\end{array}\right.$,化为x2-4kx+8=0,
△=16k2-32>0,
解得k>$\sqrt{2}$或k<-$\sqrt{2}$.
∴x1+x2=4k,x1x2=8.
直线直线AC的方程为:y-y2=-$\frac{{y}_{2}-{y}_{1}}{{x}_{2}+{x}_{1}}$(x+x2),
又∵y1=kx1-2,y2=kx2-2,
∴4ky-4k(kx2-2)=(kx2-kx1)x+kx1x2-kx22,
化为4y=(x2-x1)x+x2(4k-x2),
∵x1=4k-x2,
∴4y=(x2-x1)x+8,
令x=0,则y=2,
∴直线AC恒过一定点(0,2).
点评 本题考查点的轨迹方程的求法,考查直线的方程求法,解题时要认真审题,注意根的判别式、韦达定理、抛物线定义的合理运用,属于中档题.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
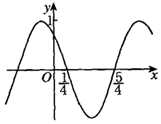 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则下列说法错误的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则下列说法错误的是( )| A. | ω=π | |
| B. | φ=$\frac{π}{4}$ | |
| C. | f(x)的单调减区间为(2k-$\frac{1}{4}$,2k+$\frac{3}{4}$),k∈Z | |
| D. | f(x)的对称中心是(k+$\frac{1}{4}$,0),k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}$ | B. | $2\sqrt{6}$ | C. | $3\sqrt{2}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.
传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.| 优秀 | 合格 | 合计 | |
| 大学组 | |||
| 中学组 | |||
| 合计 |
| P(k2≥k0) | 0.10 | 0.05 | 0.005 |
| k0 | 2.706 | 3.841 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com