
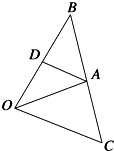
 已知O,A,B是平面上不共线的三点,直线AB上有一点C,满足2$\overrightarrow{AC}$+$\overrightarrow{CB}$=$\overrightarrow{0}$,
已知O,A,B是平面上不共线的三点,直线AB上有一点C,满足2$\overrightarrow{AC}$+$\overrightarrow{CB}$=$\overrightarrow{0}$,分析 (1)利用平面向量的加法法则即可用$\overrightarrow{OA}$,$\overrightarrow{OB}$表示$\overrightarrow{OC}$;
(2)由2$\overrightarrow{AC}$+$\overrightarrow{CB}$=$\overrightarrow{0}$,可证明A为BC的中点,点D是OB的中点,利用向量关系证明向量AD与向量OC成λ倍数关系即可得AD∥OC,那么四边形OCAD是梯形.
解答 解:(1)由题意:直线AB上有一点C,
∵2$\overrightarrow{AC}$+$\overrightarrow{CB}$=$\overrightarrow{0}$,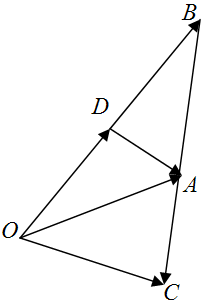
∴$\overrightarrow{CB}=2\overrightarrow{CA}$,
所以A为BC的中点;
由:$\overrightarrow{OB}+\overrightarrow{BC}=\overrightarrow{OC}$…①,
$\overrightarrow{OA}+\overrightarrow{AC}=\overrightarrow{OC}$…②,
∵$\overrightarrow{BC}=2\overrightarrow{AC}$带入①可得:$\overrightarrow{OB}+2\overrightarrow{AC}=\overrightarrow{OC}$…③
由②③消去$\overrightarrow{AC}$可得:$\overrightarrow{OC}=2\overrightarrow{OA}-\overrightarrow{OB}$.
(2)点D是OB的中点,则$\overrightarrow{OD}=\overrightarrow{DB}$=$\frac{1}{2}$$\overrightarrow{OB}$.
由:$\overrightarrow{OD}+\overrightarrow{DA}=\overrightarrow{OA}$…④
$\overrightarrow{OA}+\overrightarrow{AC}=\overrightarrow{OC}$…⑤,
由①④⑤可得:$\overrightarrow{DA}=\frac{1}{2}\overrightarrow{OC}$,
所以AD∥OC,
故得四边形OCAD是梯形.
点评 本题考查了平面向量的线性运算的应用及平面向量基本定理的应用.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $-\frac{3}{4}$ | D. | $-\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | [1,+∞) | C. | (2,+∞) | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A∪B | B. | A∩B | C. | ∁UA∩∁UB | D. | ∁UA∪∁UB |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 138万元 | B. | 134万元 | C. | 140万元 | D. | 140.25万元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com