
【题目】某人沿固定路线开车上班,沿途共有![]() 个红绿灯,他对过去
个红绿灯,他对过去![]() 个工作日上班途中的路况进行了统计,得到了如表的数据:
个工作日上班途中的路况进行了统计,得到了如表的数据:
上班路上遇见的红灯数 |
|
|
|
|
|
|
天数 |
|
|
|
|
|
|
若一路绿灯,则他从家到达公司只需用时![]() 分钟,每遇一个红灯,则会多耗时
分钟,每遇一个红灯,则会多耗时![]() 分钟,以频率作为概率的估计值
分钟,以频率作为概率的估计值
(1)试估计他平均每天上班需要用时多少分钟?
(2)若想以不少于![]() 的概率在早上
的概率在早上![]() 点前(含
点前(含![]() 点)到达公司,他最晚何时要离家去公司?
点)到达公司,他最晚何时要离家去公司?
(3)公司规定,员工应早上![]() 点(含
点(含![]() 点)前打卡考勤,否则视为迟到,每迟到一次,会被罚款
点)前打卡考勤,否则视为迟到,每迟到一次,会被罚款![]() 元.因某些客观原因,在接下来的
元.因某些客观原因,在接下来的![]() 个工作日里,他每天早上只能
个工作日里,他每天早上只能![]() 从家出发去公司,求他因迟到而被罚款的期望.
从家出发去公司,求他因迟到而被罚款的期望.
【答案】(1)![]() 分钟;(2)最晚要
分钟;(2)最晚要![]() 离家去公司;(3)
离家去公司;(3)![]() 元.
元.
【解析】
(1)将![]() 倍红灯数加
倍红灯数加![]() 作为代表值,列出该员工上班时间的频率分布表,计算出平均数即可;
作为代表值,列出该员工上班时间的频率分布表,计算出平均数即可;
(2)根据频率分布表,找到频率![]() 对应的红灯数,计算出所需时间
对应的红灯数,计算出所需时间![]() ,则他最晚在
,则他最晚在![]() 时要离家去公司;
时要离家去公司;
(3)根据出发时间,计算出他每天被处罚的概率![]() ,设罚款次数为
,设罚款次数为![]() ,则
,则![]() ,根据二项分布的期望公式计算出
,根据二项分布的期望公式计算出![]() ,即可求得罚款的期望.
,即可求得罚款的期望.
(1)依题意,上班所需时间的频率分布表如下,
上班所需时间(单位:分钟) |
|
|
|
|
|
|
天数 |
|
|
|
|
|
|
他平均每天上班需要用时为![]() 分钟;
分钟;
(2)依题意,若想以不少于![]() 的概率在早上
的概率在早上![]() 点前(含
点前(含![]() 点)到达公司,则红灯数最多为
点)到达公司,则红灯数最多为![]() ,
,
路上共用![]() 分钟,故他最晚比
分钟,故他最晚比![]() 提前
提前![]() 分钟,即最晚要
分钟,即最晚要![]() 离家去公司;
离家去公司;
(3)他每天早上只能![]() 从家出发去公司,则每天被处罚的概率为
从家出发去公司,则每天被处罚的概率为![]() ,
,
设他因迟到被罚款的次数为![]() ,则
,则![]() ,所以
,所以![]() ,
,
所以他因迟到而被罚款的期望![]() 元.
元.


科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前n项和为Sn,若
的前n项和为Sn,若![]() 为等差数列,且
为等差数列,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)是否存在正整数![]() , 使
, 使![]() 成等比数列?若存在,请求出这个等比数列;若不存在,请说明理由;
成等比数列?若存在,请求出这个等比数列;若不存在,请说明理由;
(3)若数列![]() 满足
满足![]() ,
,![]() ,且对任意的
,且对任意的![]() ,都有
,都有![]() ,求正整数k的最小值.
,求正整数k的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,点集A={(x,y)|x2+y2≤1},B={(x,y)|x≤4,y≥0,3x﹣4y≥0},则点集Q={(x,y)|x=x1+x2,y=y1+y2,(x1,y1)∈A,(x2,y2)∈B}所表示的区域的面积为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的直角顶点
的直角顶点![]() 在
在![]() 轴上,点
轴上,点![]() 为斜边
为斜边![]() 的中点,且
的中点,且![]() 平行于
平行于![]() 轴.
轴.
(Ⅰ)求点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() .以
.以![]() 为直径的圆交
为直径的圆交![]() 轴于
轴于![]() 即此圆的圆心为
即此圆的圆心为![]() ,
,![]() 求
求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C的极坐标方程为![]() 射线
射线![]() 交曲线C于点A,倾斜角为α的直线l过线段OA的中点B且与曲线C交于P、Q两点.
交曲线C于点A,倾斜角为α的直线l过线段OA的中点B且与曲线C交于P、Q两点.
(1)求曲线C的直角坐标方程及直线l的参数方程;
(2)当直线l倾斜角α为何值时, |BP|·|BQ|取最小值, 并求出|BP|·|BQ|最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中已知椭圆
中已知椭圆![]() 过点
过点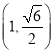 ,其左、右焦点分别为
,其左、右焦点分别为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆E的方程;
(2)若A,B分别为椭圆E的左、右顶点,动点M满足![]() ,且MA交椭圆E于点P.
,且MA交椭圆E于点P.
(i)求证:![]() 为定值;
为定值;
(ii)设PB与以PM为直径的圆的另一交点为Q,问:直线MQ是否过定点,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com