
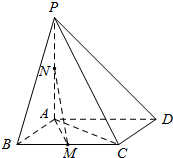
 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,点M,N分别为BC,PA的中点,且AB=AC=1,AD=$\sqrt{2}$.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,点M,N分别为BC,PA的中点,且AB=AC=1,AD=$\sqrt{2}$.分析 (Ⅰ)取PD中点Q,连接NQ、CQ,通过中位线定理可得四边形CQNM为平行四边形,利用线面平行的判定定理可得结论;
(Ⅱ)连接PM,易得∠PMA即为二面角P-BC-A的平面角,过点A在平面PAM内作AH⊥PM于H,连接CH,比较∠ACH就是直线AC与平面PBC所成的角α与∠AMH的关系计算即可得出答案.
解答  (Ⅰ)证明:取PD中点Q,连接NQ、CQ,
(Ⅰ)证明:取PD中点Q,连接NQ、CQ,
因为点M,N分别为BC,PA的中点,
所以NQ∥AD∥CM,$NQ=\frac{1}{2}AD=CM$,
∴四边形CQNM为平行四边形,∴MN∥CQ,
又MN?平面PCD,CQ⊆平面PCD,
所以MN∥平面PCD;
(Ⅱ)解:连接PM,∵AB=AC=1,点M分别为BC的中点,∴AM⊥BC,
又∵PA⊥平面ABCD,∴PM⊥BC,
∴∠PMA即为二面角P-BC-A的平面角,记为φ,
又AM∩PM=M,所以BC⊥平面PAM,则平面PBC⊥平面PAM,
过点A在平面PAM内作AH⊥PM于H,则AH⊥平面PBC.
连接CH,于是∠ACH就是直线AC与平面PBC所成的角α.
在Rt△AHM中,$AH=\frac{{\sqrt{2}}}{2}sin∠AMH$;
又∵在Rt△AHC中,AH=sinα,
∴$\frac{{\sqrt{2}}}{2}sin∠AMH=sinα$.
∵$0<α<\frac{π}{6}$,
∴$0<sinθ<\frac{1}{2}$,$0<sin∠AMH<\frac{{\sqrt{2}}}{2}$.
又$0<φ<\frac{π}{2}$,∴$0<φ<\frac{π}{4}$.
即二面角P-BC-A取值范围为$({0,\frac{π}{4}})$.
点评 本题考查中位线定理,线面平行的判定定理,作出恰当的辅助线是解决本题的关键,注意解题方法的积累,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 已知函数f(x)=$\left\{\begin{array}{l}{x,x∈[0,2]}\\{\frac{4}{x},x∈(2,4]}\end{array}\right.$
已知函数f(x)=$\left\{\begin{array}{l}{x,x∈[0,2]}\\{\frac{4}{x},x∈(2,4]}\end{array}\right.$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,过四棱柱ABCD-A1B1C1D1形木块上底面内的一点P和下底面的对角线BD将木块锯开,得到截面BDEF.
如图,过四棱柱ABCD-A1B1C1D1形木块上底面内的一点P和下底面的对角线BD将木块锯开,得到截面BDEF.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥P-ABC中,BC⊥平面APC,AB=2$\sqrt{3}$,AP=PC=CB=2.
如图,在三棱锥P-ABC中,BC⊥平面APC,AB=2$\sqrt{3}$,AP=PC=CB=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 正 | B. | 负 | C. | 零 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2}$,2] | B. | [$\frac{1}{2}$,$\sqrt{2}$] | C. | [$\frac{1}{4}$,2] | D. | [$\frac{1}{4}$,$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com