
分析 连接AI,BI,CI,设EF=2x,确定$∠CIF=\frac{B}{2}$,$∠BIC=\frac{C}{2}$.设$\frac{B}{2}$=α,$\frac{C}{2}$=β,在△CIF、△BIE中,利用正弦定理,即可得出结论.
解答  解:连接AI,BI,CI,设EF=2x,
解:连接AI,BI,CI,设EF=2x,
因为AE=AF,所以FI=EI=x,∠AIF=90°,
在△AIC中,$\frac{A}{2}+\frac{C}{2}+90°+∠CIF$=180°,$∠CIF=\frac{B}{2}$,
同理,在△AIB中,$∠BIC=\frac{C}{2}$.
设$\frac{B}{2}$=α,$\frac{C}{2}$=β,
在△CIF中,由正弦定理可得$\frac{x}{sinβ}=\frac{CF}{sinα}=\frac{3}{sinα}$①
在△BIE中,由正弦定理可得$\frac{x}{sinα}=\frac{BE}{sinβ}=\frac{4}{sinβ}$②
①×②得$\frac{{x}^{2}}{sinαsinβ}=\frac{3×4}{sinαsinβ}$,
∴x=2$\sqrt{3}$,
∴EF=4$\sqrt{3}$.
故答案为:4$\sqrt{3}$.
点评 本题考查解三角形,考查正弦定理,考查学生分析解决问题的能力,难度大.


科目:高中数学 来源: 题型:选择题
| A. | 6$\overrightarrow{a}$+2$\overrightarrow{b}$ | B. | $\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | C. | $\overrightarrow{a}$-$\frac{3}{2}$$\overrightarrow{b}$ | D. | $\overrightarrow{a}$+$\frac{3}{4}$$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
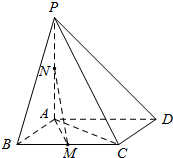 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,点M,N分别为BC,PA的中点,且AB=AC=1,AD=$\sqrt{2}$.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,点M,N分别为BC,PA的中点,且AB=AC=1,AD=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | f(x)=x2 | B. | f(x)=sinx | C. | f(x)=ex | D. | f(x)=$\frac{1}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com