
 如图,过四棱柱ABCD-A1B1C1D1形木块上底面内的一点P和下底面的对角线BD将木块锯开,得到截面BDEF.
如图,过四棱柱ABCD-A1B1C1D1形木块上底面内的一点P和下底面的对角线BD将木块锯开,得到截面BDEF.分析 (1)此题实际上是在平面A1B1C1D1形上找到过点P的线段EF,EF∥BD;
(2)欲证明平面BDEF⊥平面A1C1CA,只需证得BD⊥平面A1C1CA.
解答 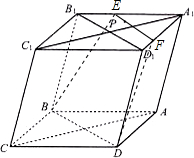 解:(1)在上底面内过点P作B1D1的平行线分别交A1D1、A1B1于F、E两点,则EF即为所作的锯线.
解:(1)在上底面内过点P作B1D1的平行线分别交A1D1、A1B1于F、E两点,则EF即为所作的锯线.
在四棱柱ABCD-A1B1C1D1中,侧棱BB1∥DD1,且BB1=DD1,
所以四边形BB1D1D是平行四边形,B1D1∥BD.
又平面ABCD∥平面A1B1C1D1,平面BDFE∩平面ABCD=BD,平面BDFE∩平面A1B1C1D1=EF,
所以EF∥BD,
从而EF∥B1D1;
(2)证明:由于四边形BB1D1D是矩形,所以BD⊥B1B.
又A1A∥B1B,
∴BD⊥A1A.
又四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,
∴BD⊥AC.
∵AC∩A1A=A,AC?平面A1C1CA,A1A?平面A1C1CA,
∴BD⊥平面A1C1CA.
∵BD?平面BDFE,
∴平面BDFE⊥平面A1C1CA.
点评 本题考查了棱柱的结构特征和平面与平面垂直的判定.解题时利用了“如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直”证得(2)的结论.


科目:高中数学 来源: 题型:解答题
 如图所示,在三棱锥D-ABC中,AB=BC=CD=1,AC=$\sqrt{3}$,平面ACD⊥平面ABC,∠BCD=90°
如图所示,在三棱锥D-ABC中,AB=BC=CD=1,AC=$\sqrt{3}$,平面ACD⊥平面ABC,∠BCD=90°查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{12}$ | B. | $\frac{1}{10}$ | C. | $\frac{2}{15}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
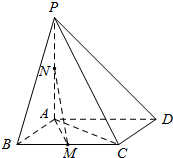 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,点M,N分别为BC,PA的中点,且AB=AC=1,AD=$\sqrt{2}$.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,点M,N分别为BC,PA的中点,且AB=AC=1,AD=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | n≤9 | B. | n≤10 | C. | n≤11 | D. | n≤12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com