Question

【题目】在直角坐标系xOy中以O为极点，x轴正半轴为极轴建立坐标系．圆C1 ， 直线C2的极坐标方程分别为ρ=4sinθ，ρcos（ ）=2 ．
（1）求C1与C2交点的极坐标；
（2）设P为C1的圆心，Q为C1与C2交点连线的中点，已知直线PQ的参数方程为 （t∈R为参数），求a，b的值．

Answer 1

【答案】
（1）解：圆C1，直线C2的直角坐标方程分别为 x2+（y﹣2）2=4，x+y﹣4=0，

解 得 或 ，

∴C1与C2交点的极坐标为（4， ）．（2 ， ）．

（2）解：由（1）得，P与Q点的坐标分别为（0，2），（1，3），

故直线PQ的直角坐标方程为x﹣y+2=0，

由参数方程可得y= x﹣ +1，

∴ ，

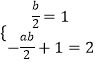解得a=﹣1，b=2．

【解析】（1）先将圆C1 ， 直线C2化成直角坐标方程，再联立方程组解出它们交点的直角坐标，最后化成极坐标即可；（2）由（1）得，P与Q点的坐标分别为（0，2），（1，3），从而直线PQ的直角坐标方程为x﹣y+2=0，由参数方程可得y= x﹣ +1，从而构造关于a，b的方程组，解得a，b的值．