
 如图,四边形ABCD中,∠CBD=α,∠C=β,∠A+β=π,AB=2,AD=1,$\sqrt{3}$BC=$\sqrt{3}$BDcosα+CDsinβ
如图,四边形ABCD中,∠CBD=α,∠C=β,∠A+β=π,AB=2,AD=1,$\sqrt{3}$BC=$\sqrt{3}$BDcosα+CDsinβ分析 (1)条件化为$\sqrt{3}$sin(α+β)=$\sqrt{3}$sinβcosα+sinαsinβ,即可求角β的大小;(Ⅱ)求出CB+CD≤2$\sqrt{7}$,即可求四边形ABCD周长的取值范围.
解答 解:(1)∵$\sqrt{3}$BC=$\sqrt{3}$BDcosα+CDsinβ,
∴$\sqrt{3}$sin∠BDC=$\sqrt{3}$sinβcosα+sinαsinβ,
∴$\sqrt{3}$sin(α+β)=$\sqrt{3}$sinβcosα+sinαsinβ,
化简可得tanβ=$\sqrt{3}$,∴β=$\frac{π}{3}$;
(2)由题意,∠BAD=$\frac{2π}{3}$,BD=$\sqrt{4+1-2×2×1×(-\frac{1}{2})}$=7,
∵BD2=CB2+CD2-2CB•CD•cosβ=(CB+CD)2-3CB•CD≥$\frac{{(CB+CD)}^{2}}{4}$,
∴CB+CD≤2$\sqrt{7}$,∵CB+CD>$\sqrt{7}$,
∴四边形ABCD周长的取值范围(3+$\sqrt{7}$,3+2$\sqrt{7}$).
点评 本题考查三角函数的化简,考查余弦定理的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{3π}{4}$ | C. | $\frac{5π}{6}$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{3π}{2}$+1+$\frac{\sqrt{3}}{2}$ | B. | 3π+$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$ | C. | $\frac{3π+1+\sqrt{3}}{2}$ | D. | 3π+1+$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
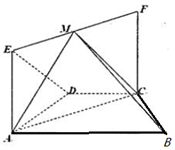 如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=2,∠ABC=60°,四边形ACFE为矩形,CF=$\sqrt{3}$,平面ACFE⊥平面ABCD,点M为线段EF中点.
如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=2,∠ABC=60°,四边形ACFE为矩形,CF=$\sqrt{3}$,平面ACFE⊥平面ABCD,点M为线段EF中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
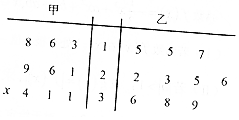 甲、乙两名篮球运动员在10场比赛中得分的茎叶图如图所示,则“x=9”是“甲运动员得分平均数大于乙运动员得分平均数”的( )
甲、乙两名篮球运动员在10场比赛中得分的茎叶图如图所示,则“x=9”是“甲运动员得分平均数大于乙运动员得分平均数”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1d>0,dS4>0 | B. | a1d>0,dS4<0 | C. | a1d<0,dS4>0 | D. | a1d<0,dS4<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com