
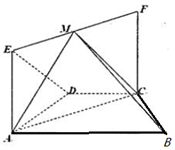
 如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=2,∠ABC=60°,四边形ACFE为矩形,CF=$\sqrt{3}$,平面ACFE⊥平面ABCD,点M为线段EF中点.
如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=2,∠ABC=60°,四边形ACFE为矩形,CF=$\sqrt{3}$,平面ACFE⊥平面ABCD,点M为线段EF中点.分析 (Ⅰ)取AC的中点N,连接DN,EN.说明∠DEN为异面直线ED与MC所成的角.在Rt△EDN中,求解即可.
(Ⅱ)证明AC⊥BC,推出BC⊥平面ACFE,得到BC⊥AM.AM⊥MC,即可证明AM⊥平面MBC,平面AMB⊥平面MBC.
(Ⅲ)过点C作CH⊥MB=H,∠CBH为直线BC与平面AMB所成的角.在Rt△BCM中,求解直线BC与平面AMB所成角的正弦值.
解答 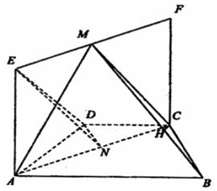 (Ⅰ)解:取AC的中点N,连接DN,EN.
(Ⅰ)解:取AC的中点N,连接DN,EN.
∵四边形ACFE为矩形,M为线段EF中点,
∴EM∥NC且EM=NC,
∴EN∥MC,
∴∠DEN为异面直线ED与MC所成的角.
在△ADC中,AD=DC=2,∠ADC=120°,
∴DN=1且DN⊥AC,
又∵平面ACFE⊥平面ABCD,
∴DN⊥平面ACFE,
∴DN⊥EN.
在Rt△EDN中,$EN=\sqrt{6}$,$tan∠DEN=\frac{DN}{EN}=\frac{{\sqrt{6}}}{6}$.
(Ⅱ)证明:在△ABC中,∠ABC=60°,BC=2,$AC=2\sqrt{3}$,
∴AC⊥BC,
又∵平面ACFE⊥平面ABCD,
∴BC⊥平面ACFE,
∴BC⊥AM.
在矩形ACFE中,∵$AM=MC=\sqrt{6}$,$AC=2\sqrt{3}$,
∴AM⊥MC,
又∵BC∩MC=C,
∴AM⊥平面MBC,
又∵AM?平面AMB,
∴平面AMB⊥平面MBC.
(Ⅲ)解:过点C作CH⊥MB=H,
由第(Ⅱ)问知平面AMB⊥平面MBC=MB,
∴CH⊥平面AMB,
∴∠CBH为直线BC与平面AMB所成的角.
在Rt△BCM中,$MC=\sqrt{6}$,BC=2,
∴$MB=\sqrt{10}$,∴$CH=\frac{BC•MC}{MB}=\frac{{2\sqrt{15}}}{5}$,
∴$sin∠CBH=\frac{CH}{CB}=\frac{{\sqrt{15}}}{5}$,
∴直线BC与平面AMB所成角的正弦值为$\frac{{\sqrt{15}}}{5}$.
点评 本题考查直线与平面垂直的判定定理以及性质定理的应用,直线与平面所成角的求法,异面直线所成角的求法,考查空间想象能力以及计算能力.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD中,∠CBD=α,∠C=β,∠A+β=π,AB=2,AD=1,$\sqrt{3}$BC=$\sqrt{3}$BDcosα+CDsinβ
如图,四边形ABCD中,∠CBD=α,∠C=β,∠A+β=π,AB=2,AD=1,$\sqrt{3}$BC=$\sqrt{3}$BDcosα+CDsinβ查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1) | B. | [-1,2) | C. | [-2,2) | D. | [0,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com