考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积,直线与平面所成的角
专题:空间位置关系与距离
分析:(1)先证明四边形AOED是平行四边形,即可得到 DE∥OA,从而证得DE∥面ABC.
(2)由CA⊥AB,且AA
1⊥CA,可得CA⊥面AA
1B
1B,即CA为四棱锥的高,设圆柱高为h,底半径为r,则V
柱=πr
2h,求出椎体的体积,即可得到四棱锥C-ABB
1A
1与圆柱OO
1的体积比.
(3)先证 A
1O
1⊥面CBB
1C
1,则∠A
1CO
1为CA
1与面BB
1C所成的角,在Rt△A
1O
1C中,由sin∠A
1CO
1=
求得CA
1与面BB
1C所成角的正弦值.
解答:
解:(1)证明:连接EO,OA.∵E,O分别为B
1C,BC的中点,∴EO∥BB
1.
又DA∥BB
1,且DA=EO=
BB
1.∴四边形AOED是平行四边形,
即DE∥OA,DE?面ABC.∴DE∥面ABC.
(2)由题DE⊥面CBB
1,且由(1)知DE∥OA.∴AO⊥面CBB
1,∴AO⊥BC,
∴AC=AB.因BC是底面圆O的直径,得CA⊥AB,且AA
1⊥CA,
∴CA⊥面AA
1B
1B,即CA为四棱锥的高.
设圆柱高为h,底半径为r,则V
柱=πr
2h,V
锥=
h•(
r)•(
r)=
hr
2,
∴V
锥:V
柱 =
.
(3)解:作过C的母线CC
1,连接B
1C
1,则B
1C
1是上底面圆O
1的直径,
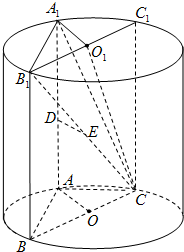
连接A
1O
1,得A
1O
1∥AO,又AO⊥面CBB
1C
1,
∴A
1O
1⊥面CBB
1C
1,连接CO
1,
则∠A
1CO
1为CA
1与面BB
1C所成的角,
设BB
1=BC=2,则A
1C=
,
A
1O
1=1.(12分)
在Rt△A
1O
1C中,sin∠A
1CO
1=
=
.
点评:本题考查证明线面平行的方法,求棱锥的体积和直线与平面成的角,找出∠A1CO1为CA1与面BB1C所成的角,是解题的难点.

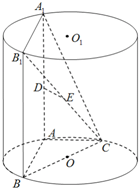 如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D,E分别是AA1、CB1的中点,DE⊥面CBB1.
如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D,E分别是AA1、CB1的中点,DE⊥面CBB1.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案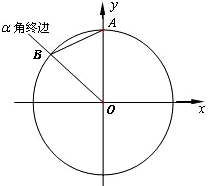 如图所示,单位圆(半径为1)的圆心O为坐标原点,它与y轴的正半轴交于点A,与钝角α的终边交于点B(xB,yB),设∠BAO=β,sin2β=
如图所示,单位圆(半径为1)的圆心O为坐标原点,它与y轴的正半轴交于点A,与钝角α的终边交于点B(xB,yB),设∠BAO=β,sin2β=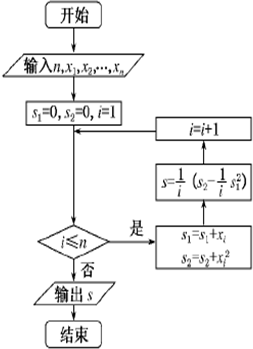 某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中n位居民的月均用水量分别为x1,…,xn(单位:吨).根据如图所示的程序框图,若n=2,且x1,x2分别为1,2,则输出的结果s为
某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中n位居民的月均用水量分别为x1,…,xn(单位:吨).根据如图所示的程序框图,若n=2,且x1,x2分别为1,2,则输出的结果s为