
分析 由f(x)求导,确定出g(x),对g(x)求导,对a进行讨论,分情况来看单调区间.
解答 解:∵f(x)=(x+1)lnx-a(x+1),定义域为(0,+∞),
∴f′(x)=lnx+1+$\frac{1}{x}$-a,
∴g(x)=lnx+1-a+$\frac{1-a}{x}$,定义域为(0,+∞),
∵g′(x)=$\frac{x-(1-a)}{{x}^{2}}$,
①a≥1时,g′(x)≥0恒成立,
∴g(x)在(0,+∞)上单调递增,
②a<1时,g′(x)=0得x=1-a,
∴g(x)在区间(0,1-a)上单调递减,
在区间(1-a,+∞)上单调递增,
综上所述:a≥1时,g(x)的单调增区间是(0,+∞),
a<1时,g(x)的单调增区间是(1-a,+∞),
单调减区间是(0,1-a).
点评 本题考查分类讨论来看单调区间,时高考题目中经常考查的点.


科目:高中数学 来源: 题型:解答题
 已知抛物线C:x2=4y的焦点为F,准线与y轴的交点为Q,过点Q的直线l与抛物线C相交于不同的A,B两点.
已知抛物线C:x2=4y的焦点为F,准线与y轴的交点为Q,过点Q的直线l与抛物线C相交于不同的A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “p或q”为真,“非p”为假 | B. | “p且q”为假,“非q”为真 | ||
| C. | “p且q”为假,“非p”为假 | D. | “p且q”为真,“p或q”为真 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)在[a,b]上可导 | |
| B. | ${∫}_{a}^{x}$f(t)dt为f(x)在[a,b]上的一个原函数: | |
| C. | ${∫}_{x}^{b}$f(t)dt为f(x)在[a,b]上的一个原函数 | |
| D. | f(x)在[a,b]上至少有一个零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,-π<φ≤π)的图象如图所示,则函数f(x)的解析式为2sin($\frac{11}{6}$x-$\frac{5π}{6}$).
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,-π<φ≤π)的图象如图所示,则函数f(x)的解析式为2sin($\frac{11}{6}$x-$\frac{5π}{6}$).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
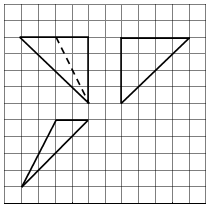
| A. | 8+8$\sqrt{2}$+4$\sqrt{6}$ | B. | 8+8$\sqrt{2}$+2$\sqrt{6}$ | C. | 2+2$\sqrt{2}$+$\sqrt{6}$ | D. | $\frac{1}{2}$+$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{6}}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com