
分析 (1)由偶次根式非负,可得函数的定义域;
(2)运用单调性的定义,设自变量、作差,变形(运用分子有理化),定符号和下结论;
(3)由单调性,即可得到最小值.
解答 解:(1)由函数f(x)=$\sqrt{x+1}$可得
x+1≥0,解得x≥-1,
则定义域为[-1,+∞);
(2)证明:设-1≤x1<x2,
则f(x1)-f(x2)=$\sqrt{1+{x}_{1}}$-$\sqrt{1+{x}_{2}}$
=$\frac{{x}_{1}-{x}_{2}}{\sqrt{1+{x}_{1}}+\sqrt{1+{x}_{2}}}$,
由-1≤x1<x2,
可得x1-x2<0,$\sqrt{1+{x}_{1}}$+$\sqrt{1+{x}_{2}}$>0,
即有f(x1)-f(x2)<0,
即为f(x1)<f(x2),
故f(x)在[-1,+∞)递增;
(3)由x≥-1,可得$\sqrt{1+x}$≥0,
即有x=-1时,函数取得最小值,且为0.
点评 本题考查函数的定义域的求法和单调性的证明及应用:求最值,考查运算能力,属于基础题.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
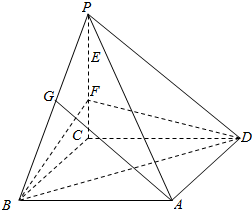 如图,在四棱锥P-ABCD中,已知底面ABCD是平行四边形,E、F是PC的三等分点,G是PB的中点,过E,A,G三点的平面?FBD是否平行?
如图,在四棱锥P-ABCD中,已知底面ABCD是平行四边形,E、F是PC的三等分点,G是PB的中点,过E,A,G三点的平面?FBD是否平行?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com