练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知数列{an}中,a1=1,前n项和S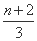n=an.

    (1)求a2,a3;

    (2)求{an}的通项公式.


    解:(1)由S2=a2得3(a1+a2)=4a2,解得a2=3a1=3,

    由S3=a3得3(a1+a2+a3)=5a3,

    解得a3= (a1+a2)=6.

    (2)由题设知a1=1.

    当n>1时有an=Sn-Sn-1=an-an-1,

    整理得an=an-1,

    于是a1=1,

    a2=a1,

    a3=a2,

    …

    an-1=an-2,

    an=an-1.

    将以上n个等式两端分别相乘,整理得an=.

    综上,{an}的通项公式an=.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知抛物线方程x2＝4y，过点P(t，－4)作抛物线的两条切线PA、PB，切点分别为A、B.

    (1)求证：直线AB过定点(0,4)；

    (2)求△OAB(O为坐标原点)面积的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    等比数列{an}的前n项和为Sn,若S3+3S2=0,则公比q=　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    数列{an}满足a1=2,且对任意的m,n∈N*,都有=an,则a3=　　　　;{an}的前n项和Sn=　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在等比数列{an}中,an>0,且a1·a2…a7·a8=16,则a4+a5的最小值为　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    正项数列{an}满足-(2n-1)an-2n=0.

    (1)求数列{an}的通项公式an;

    (2)令bn=,求数列{bn}的前n项和Tn.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}的通项公式是an=,那么这个数列是(　　)

    (A)递增数列 (B)递减数列

    (C)摆动数列 (D)常数列

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)是奇函数,g(x)是偶函数,且f(-1)+g(1)=2,f(1)+g(-1)=4,则g(1)等于(　　)

    (A)4    (B)3    (C)2    (D)1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在实数的原有运算法则中,我们补充定义新运算“⊕”;当a≥b时,a⊕b=a;当a<b时,a⊕b=b2,函数f(x)=(1⊕x)·x(其中“·”仍为通常的乘法),则函数f(x)在[0,2]上的值域为(　　)

    (A)[0,4]    (B)[1,4]    (C)[0,8]    (D)[1,8]

    查看答案和解析>>

    同步练习册答案