
| A. | 相交 | B. | 相离 | C. | 相交或相切 | D. | 相切或相离 |
分析 根据点A,B在曲线y=$\sqrt{x}$上不同两点,从而设出A,B坐标:A(${x}_{1},\sqrt{{x}_{1}}$),$B({x}_{2},\sqrt{{x}_{2}})$,而由$\overrightarrow{OA}$•$\overrightarrow{OB}$=6可得到x1x2=4,能够写出直线AB的方程,从而求出圆心即原点到直线AB的距离和圆半径$\frac{2}{3}$比较即可判断出直线和圆的位置关系.
解答 解:设A(${x}_{1},\sqrt{{x}_{1}}$),$B({x}_{2},\sqrt{{x}_{2}})$;
∴由$\overrightarrow{OA}•\overrightarrow{OB}=6$得:
${x}_{1}{x}_{2}+\sqrt{{x}_{1}{x}_{2}}=6$,设$\sqrt{{x}_{1}{x}_{2}}=t,t>0$,则:
t2+t-6=0,解得t=2,或t=-3(舍去);
∴x1x2=4;
直线AB的斜率为k=$\frac{\sqrt{{x}_{2}}-\sqrt{{x}_{1}}}{{x}_{2}-{x}_{1}}=\frac{1}{\sqrt{{x}_{2}}+\sqrt{{x}_{1}}}$;
∴直线AB的方程为:$y-\sqrt{{x}_{2}}=\frac{1}{\sqrt{{x}_{2}}+\sqrt{{x}_{1}}}(x-{x}_{2})$;
∴原点到该直线的距离为$\frac{|\frac{{x}_{2}}{\sqrt{{x}_{2}}+\sqrt{{x}_{1}}}-\sqrt{{x}_{2}}|}{\sqrt{(\frac{1}{\sqrt{{x}_{2}}+\sqrt{{x}_{1}}})^{2}+1}}$=$\frac{2}{\sqrt{{x}_{1}+{x}_{2}+5}}$$<\frac{2}{3}$;
∴直线AB与圆${x}^{2}+{y}^{2}=\frac{4}{9}$的位置关系为相交.
故选A.
点评 考查根据曲线方程设出曲线上点的坐标的方法,数量积的坐标运算,解一元二次方程,以及由两点坐标写直线方程,点到直线的距离公式,直线和圆的位置关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
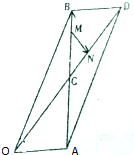 如图,平行四边形OADB的对角线OD、AB相交于点C,线段BC上有一点M满足BC=3BM,线段CD上有一点N满足CD=3CN,设|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=6,∠AOB=60°.
如图,平行四边形OADB的对角线OD、AB相交于点C,线段BC上有一点M满足BC=3BM,线段CD上有一点N满足CD=3CN,设|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=6,∠AOB=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,0)∪(3,4] | B. | (-4,-3)∪(1,2)∪(2,3) | C. | (-1,0)∪(1,2)∪(2,3) | D. | (-4,-3)∪(-1,0)∪(1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com