
函数f(x)=sin2x+2cosx在区间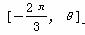 上的最大值为1,
上的最大值为1, 则θ的值是________.
则θ的值是________.
科目:高中数学 来源: 题型:
已知数列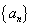 的前
的前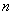 项和为
项和为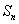
(1)若数列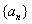 是等比数列,满足
是等比数列,满足 ,
, 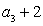 是
是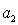 ,
,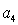 的等差
的等差 中项,求数列
中项,求数列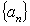 的通项公式;
的通项公式;
(2)是否存在等差数列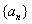 ,使对任意
,使对任意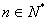 都有
都有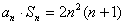 ?若存在,请求出所有满足条件的等差数列;若不存在,请说明理由.
?若存在,请求出所有满足条件的等差数列;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=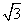 sin(ωx+φ)-cos(ωx+φ)(0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
sin(ωx+φ)-cos(ωx+φ)(0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为 .
.
(1)求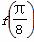 的值;
的值;
(2)将函数y=f(x)的图象向右平移 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
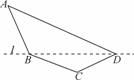
某单位设计一个展览沙盘,现欲在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示,为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求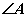 和
和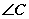 互补,且AB=BC
互补,且AB=BC
(1) 设AB=x米,cosA=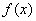 ,求
,求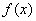 的解析式,并指出x的取值范围.
的解析式,并指出x的取值范围.
(2) 求四边形ABCD面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com