
 如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°,E是PD的中点.
如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°,E是PD的中点.分析 (1)取PA的中点F,连接EF,BF,通过证明CE∥BF,利用直线与平面平行的判定定理证明即可.
(2)利用已知条件转化求解M到底面的距离,作出二面角的平面角,然后求解二面角M-AB-D的余弦值即可.
解答 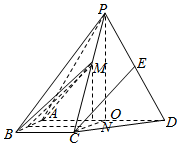
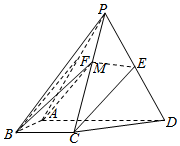 (1)证明:取PA的中点F,连接EF,BF,因为E是PD的中点,
(1)证明:取PA的中点F,连接EF,BF,因为E是PD的中点,
所以EF$\underset{∥}{=}$$\frac{1}{2}$AD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°,∴BC∥$\frac{1}{2}$AD,
∴BCEF是平行四边形,可得CE∥BF,BF?平面PAB,CE?平面PAB,
∴直线CE∥平面PAB;
(2)解:四棱锥P-ABCD中,
侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,
∠BAD=∠ABC=90°,E是PD的中点.
取AD的中点O,M在底面ABCD上的射影N在OC上,设AD=2,则AB=BC=1,OP=$\sqrt{3}$,
∴∠PCO=60°,直线BM与底面ABCD所成角为45°,
可得:BN=MN,CN=$\frac{\sqrt{3}}{3}$MN,BC=1,
可得:1+$\frac{1}{3}$BN2=BN2,BN=$\frac{\sqrt{6}}{2}$,MN=$\frac{\sqrt{6}}{2}$,
作NQ⊥AB于Q,连接MQ,
所以∠MQN就是二面角M-AB-D的平面角,MQ=$\sqrt{{1}^{2}+(\frac{\sqrt{6}}{2})^{2}}$
=$\frac{\sqrt{10}}{2}$,
二面角M-AB-D的余弦值为:$\frac{1}{\frac{\sqrt{10}}{2}}$=$\frac{\sqrt{10}}{5}$.
点评 本题考查直线与平面平行的判定定理的应用,二面角的平面角的求法,考查空间想象能力以及计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
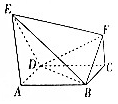 如图,正方形ABCD的边长为1,E,F是平面ABCD同一侧的两点,AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,FC=$\frac{1}{2}$.
如图,正方形ABCD的边长为1,E,F是平面ABCD同一侧的两点,AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,FC=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
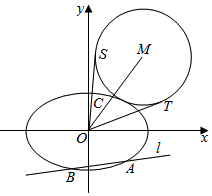 在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,焦距为2.
在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,焦距为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com