
分析 (1)分别求得a1=1,a2=2,a3=3,b1=1,b2=3,b3=5,代入即可求得c1,c2,c3;由(bk-nak)-(b1-na1)≤0,则b1-na1≥bk-nak,则cn=b1-na1=1-n,cn+1-cn=-1对?n∈N*均成立;
(2)由bi-ain=[b1+(i-1)d1]-[a1+(i-1)d2]×n=(b1-a1n)+(i-1)(d2-d1×n),分类讨论d1=0,d1>0,d1<0三种情况进行讨论根据等差数列的性质,即可求得使得cm,cm+1,cm+2,…是等差数列;设$\frac{{c}_{n}}{n}$=An+B+$\frac{C}{n}$对任意正整数M,存在正整数m,使得n≥m,$\frac{{c}_{n}}{n}$>M,分类讨论,采用放缩法即可求得因此对任意正数M,存在正整数m,使得当n≥m时,$\frac{{c}_{n}}{n}$>M.
解答 解:(1)a1=1,a2=2,a3=3,b1=1,b2=3,b3=5,
当n=1时,c1=max{b1-a1}=max{0}=0,
当n=2时,c2=max{b1-2a1,b2-2a2}=max{-1,-1}=-1,
当n=3时,c3=max{b1-3a1,b2-3a2,b3-3a3}=max{-2,-3,-4}=-2,
下面证明:对?n∈N*,且n≥2,都有cn=b1-na1,
当n∈N*,且2≤k≤n时,
则(bk-nak)-(b1-na1),
=[(2k-1)-nk]-1+n,
=(2k-2)-n(k-1),
=(k-1)(2-n),由k-1>0,且2-n≤0,
则(bk-nak)-(b1-na1)≤0,则b1-na1≥bk-nak,
因此,对?n∈N*,且n≥2,cn=b1-na1=1-n,
cn+1-cn=-1,
∴c2-c1=-1,
∴cn+1-cn=-1对?n∈N*均成立,
∴数列{cn}是等差数列;
(2)证明:设数列{an}和{bn}的公差分别为d1,d2,下面考虑的cn取值,
由b1-a1n,b2-a2n,…,bn-ann,
考虑其中任意bi-ain,(i∈N*,且1≤i≤n),
则bi-ain=[b1+(i-1)d1]-[a1+(i-1)d2]×n,
=(b1-a1n)+(i-1)(d2-d1×n),
下面分d1=0,d1>0,d1<0三种情况进行讨论,
①若d1=0,则bi-ain═(b1-a1n)+(i-1)d2,
当若d2≤0,则(bi-ain)-(b1-a1n)=(i-1)d2≤0,
则对于给定的正整数n而言,cn=b1-a1n,此时cn+1-cn=-a1,
∴数列{cn}是等差数列;
当d2>0,(bi-ain)-(bn-ann)=(i-n)d2>0,
则对于给定的正整数n而言,cn=bn-ann=bn-a1n,
此时cn+1-cn=d2-a1,
∴数列{cn}是等差数列;
此时取m=1,则c1,c2,…,是等差数列,命题成立;
②若d1>0,则此时-d1n+d2为一个关于n的一次项系数为负数的一次函数,
故必存在m∈N*,使得n≥m时,-d1n+d2<0,
则当n≥m时,(bi-ain)-(b1-a1n)=(i-1)(-d1n+d2)≤0,(i∈N*,1≤i≤n),
因此当n≥m时,cn=b1-a1n,
此时cn+1-cn=-a1,故数列{cn}从第m项开始为等差数列,命题成立;
③若d1<0,此时-d1n+d2为一个关于n的一次项系数为正数的一次函数,
故必存在s∈N*,使得n≥s时,-d1n+d2>0,
则当n≥s时,(bi-ain)-(bn-ann)=(i-1)(-d1n+d2)≤0,(i∈N*,1≤i≤n),
因此,当n≥s时,cn=bn-ann,
此时=$\frac{{b}_{n}-{a}_{n}n}{n}$=-an+$\frac{{b}_{n}}{n}$,
=-d2n+(d1-a1+d2)+$\frac{{b}_{1}-{d}_{2}}{n}$,
令-d1=A>0,d1-a1+d2=B,b1-d2=C,
下面证明:$\frac{{c}_{n}}{n}$=An+B+$\frac{C}{n}$对任意正整数M,存在正整数m,使得n≥m,$\frac{{c}_{n}}{n}$>M,
若C≥0,取m=[$\frac{丨M-B丨}{A}$+1],[x]表示不大于x的最大整数,
当n≥m时,$\frac{{c}_{n}}{n}$≥An+B≥Am+B=A[$\frac{丨M-B丨}{A}$+1]+B>A•$\frac{M-B}{A}$+B=M,
此时命题成立;
若C<0,取m=[$\frac{丨M-C-B丨}{A}$]+1,
当n≥m时,
$\frac{{c}_{n}}{n}$≥An+B+$\frac{C}{n}$≥Am+B+C>A•$\frac{丨M-C-B丨}{A}$+B+C$≥\\;M-C-B+B+C$≥M-C-B+B+C=M,
此时命题成立,
因此对任意正数M,存在正整数m,使得当n≥m时,$\frac{{c}_{n}}{n}$>M;
综合以上三种情况,命题得证.
点评 本题考查数列的综合应用,等差数列的性质,考查与不等式的综合应用,考查“放缩法”的应用,考查学生分析问题及解决问题的能力,考查分类讨论及转化思想,考查计算能力,属于难题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
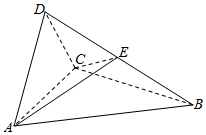 如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
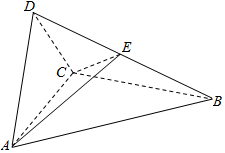 如图四面体ABCD中,△ABC是正三角形,AD=CD.
如图四面体ABCD中,△ABC是正三角形,AD=CD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中Ai的横、纵坐标分别为第i名工人上午的工作时间和加工的零件数,点Bi的横、纵坐标分别为第i名工人下午的工作时间和加工的零件数,i=1,2,3.
三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中Ai的横、纵坐标分别为第i名工人上午的工作时间和加工的零件数,点Bi的横、纵坐标分别为第i名工人下午的工作时间和加工的零件数,i=1,2,3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{15}}{5}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°,E是PD的中点.
如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°,E是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+$\frac{1}{b}$<$\frac{b}{{2}^{a}}$<log2(a+b)) | B. | $\frac{b}{{2}^{a}}$<log2(a+b)<a+$\frac{1}{b}$ | ||
| C. | a+$\frac{1}{b}$<log2(a+b)<$\frac{b}{{2}^{a}}$ | D. | log2(a+b))<a+$\frac{1}{b}$<$\frac{b}{{2}^{a}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com