
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{15}}{5}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 【解法一】设M、N、P分别为AB,BB1和B1C1的中点,得出AB1、BC1夹角为MN和NP夹角或其补角;根据中位线定理,结合余弦定理求出AC、MQ,MP和∠MNP的余弦值即可.
【解法二】通过补形的办法,把原来的直三棱柱变成直四棱柱,解法更简洁.
解答 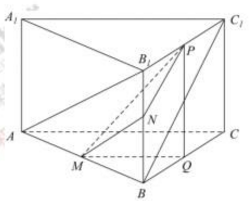 解:【解法一】如图所示,设M、N、P分别为AB,BB1和B1C1的中点,
解:【解法一】如图所示,设M、N、P分别为AB,BB1和B1C1的中点,
则AB1、BC1夹角为MN和NP夹角或其补角
(因异面直线所成角为(0,$\frac{π}{2}$]),
可知MN=$\frac{1}{2}$AB1=$\frac{\sqrt{5}}{2}$,
NP=$\frac{1}{2}$BC1=$\frac{\sqrt{2}}{2}$;
作BC中点Q,则△PQM为直角三角形;
∵PQ=1,MQ=$\frac{1}{2}$AC,
△ABC中,由余弦定理得
AC2=AB2+BC2-2AB•BC•cos∠ABC
=4+1-2×2×1×(-$\frac{1}{2}$)
=7,
∴AC=$\sqrt{7}$,
∴MQ=$\frac{\sqrt{7}}{2}$;
在△MQP中,MP=$\sqrt{{MQ}^{2}{+PQ}^{2}}$=$\frac{\sqrt{11}}{2}$;
在△PMN中,由余弦定理得
cos∠MNP=$\frac{{MN}^{2}{+NP}^{2}{-PM}^{2}}{2•MH•NP}$=$\frac{{(\frac{\sqrt{5}}{2})}^{2}{+(\frac{\sqrt{2}}{2})}^{2}{-(\frac{\sqrt{11}}{2})}^{2}}{2×\frac{\sqrt{5}}{2}×\frac{\sqrt{2}}{2}}$=-$\frac{\sqrt{10}}{5}$;
又异面直线所成角的范围是(0,$\frac{π}{2}$],
∴AB1与BC1所成角的余弦值为$\frac{\sqrt{10}}{5}$.
【解法二】如图所示,
补成四棱柱ABCD-A1B1C1D1,求∠BC1D即可;
BC1=$\sqrt{2}$,BD=$\sqrt{{2}^{2}{+1}^{2}-2×2×1×cos60°}$=$\sqrt{3}$,
C1D=$\sqrt{5}$,
∴${{BC}_{1}}^{2}$+BD2=${{C}_{1}D}^{2}$,
∴∠DBC1=90°,
∴cos∠BC1D=$\frac{\sqrt{2}}{\sqrt{5}}$=$\frac{\sqrt{10}}{5}$.
点评 本题考查了空间中的两条异面直线所成角的计算问题,也考查了空间中的平行关系应用问题,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
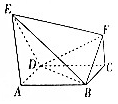 如图,正方形ABCD的边长为1,E,F是平面ABCD同一侧的两点,AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,FC=$\frac{1}{2}$.
如图,正方形ABCD的边长为1,E,F是平面ABCD同一侧的两点,AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,FC=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 随机变量ξ,η满足η=2ξ+3,则其方差的关系为D(η)=4D(ξ) | |
| B. | 回归分析中,R2的值越大,说明残差平方和越小 | |
| C. | 画残差图时,纵坐标一定为残差,横坐标一定为编号 | |
| D. | 回归直线一定过样本点中心 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com