
分析 (Ⅰ)利用已知条件求出等差数列的公差,然后求{an}的通项公式;
(Ⅱ)利用已知条件求出公比,然后求解数列的和即可.
解答 解:(Ⅰ)等差数列{an},a1=1,a2+a4=10,可得:1+d+1+3d=10,解得d=2,
所以{an}的通项公式:an=1+(n-1)×2=2n-1.
(Ⅱ)由(Ⅰ)可得a5=a1+4d=9,
等比数列{bn}满足b1=1,b2b4=9.可得b3=3,或-3(舍去)(等比数列奇数项符号相同).
∴q2=3,
{b2n-1}是等比数列,公比为3,首项为1.
b1+b3+b5+…+b2n-1=$\frac{1(1-{q}^{2n})}{1-{q}^{2}}$=$\frac{{3}^{n}-1}{2}$.
点评 本题考查等差数列与等比数列的应用,数列求和以及通项公式的求解,考查计算能力.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移$\frac{π}{6}$个单位长度,得到曲线C2 | |
| B. | 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移$\frac{π}{12}$个单位长度,得到曲线C2 | |
| C. | 把C1上各点的横坐标缩短到原来的$\frac{1}{2}$倍,纵坐标不变,再把得到的曲线向右平移$\frac{π}{6}$个单位长度,得到曲线C2 | |
| D. | 把C1上各点的横坐标缩短到原来的$\frac{1}{2}$倍,纵坐标不变,再把得到的曲线向左平移$\frac{π}{12}$个单位长度,得到曲线C2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{7}{9}$ | B. | -$\frac{2}{9}$ | C. | $\frac{2}{9}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
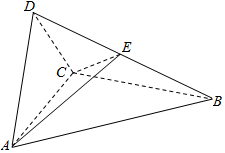 如图四面体ABCD中,△ABC是正三角形,AD=CD.
如图四面体ABCD中,△ABC是正三角形,AD=CD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{15}}{5}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
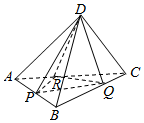 如图,已知正四面体D-ABC(所有棱长均相等的三棱锥),P、Q、R分别为AB、BC、CA上的点,AP=PB,$\frac{BQ}{QC}$=$\frac{CR}{RA}$=2,分别记二面角D-PR-Q,D-PQ-R,D-QR-P的平面角为α、β、γ,则( )
如图,已知正四面体D-ABC(所有棱长均相等的三棱锥),P、Q、R分别为AB、BC、CA上的点,AP=PB,$\frac{BQ}{QC}$=$\frac{CR}{RA}$=2,分别记二面角D-PR-Q,D-PQ-R,D-QR-P的平面角为α、β、γ,则( )| A. | γ<α<β | B. | α<γ<β | C. | α<β<γ | D. | β<γ<α |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com