
分析 设等比数列{an}的公比为q≠1,S3=$\frac{7}{4}$,S6=$\frac{63}{4}$,可得$\frac{{a}_{1}(1-{q}^{3})}{1-q}$=$\frac{7}{4}$,$\frac{{a}_{1}(1-{q}^{6})}{1-q}$=$\frac{63}{4}$,联立解出即可得出.
解答 解:设等比数列{an}的公比为q≠1,
∵S3=$\frac{7}{4}$,S6=$\frac{63}{4}$,∴$\frac{{a}_{1}(1-{q}^{3})}{1-q}$=$\frac{7}{4}$,$\frac{{a}_{1}(1-{q}^{6})}{1-q}$=$\frac{63}{4}$,
解得a1=$\frac{1}{4}$,q=2.
则a8=$\frac{1}{4}×{2}^{7}$=32.
故答案为:32.
点评 本题考查了等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
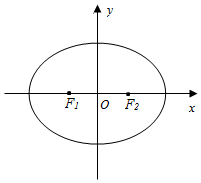 如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,离心率为$\frac{1}{2}$,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.
如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,离心率为$\frac{1}{2}$,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
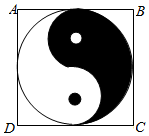 如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )
如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{π}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
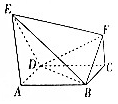 如图,正方形ABCD的边长为1,E,F是平面ABCD同一侧的两点,AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,FC=$\frac{1}{2}$.
如图,正方形ABCD的边长为1,E,F是平面ABCD同一侧的两点,AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,FC=$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com