
分析 (1)将曲线C的参数方程化为标准方程,直线l的参数方程化为一般方程,联立两方程可以求得焦点坐标;
(2)曲线C上的点可以表示成P(3cosθ,sinθ),θ∈[0,2π),运用点到直线距离公式可以表示出P到直线l的距离,再结合距离最大值为$\sqrt{17}$进行分析,可以求出a的值.
解答 解:(1)曲线C的参数方程为$\left\{\begin{array}{l}{x=3cosθ}\\{y=sinθ}\end{array}\right.$(θ为参数),化为标准方程是:$\frac{{x}^{2}}{9}$+y2=1;
a=-1时,直线l的参数方程化为一般方程是:x+4y-3=0;
联立方程$\left\{\begin{array}{l}{\frac{{x}^{2}}{9}+{y}^{2}=1}\\{x+4y-3=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{21}{25}}\\{y=\frac{24}{25}}\end{array}\right.$,
所以椭圆C和直线l的交点为(3,0)和(-$\frac{21}{25}$,$\frac{24}{25}$).
(2)l的参数方程$\left\{\begin{array}{l}{x=a+4t}\\{y=1-t}\end{array}\right.$(t为参数)化为一般方程是:x+4y-a-4=0,
椭圆C上的任一点P可以表示成P(3cosθ,sinθ),θ∈[0,2π),
所以点P到直线l的距离d为:
d=$\frac{|3cosθ+4sinθ-a-4|}{\sqrt{17}}$=$\frac{|5sin(θ+φ)-a-4|}{\sqrt{17}}$,φ满足tanφ=$\frac{3}{4}$,且的d的最大值为$\sqrt{17}$.
①当-a-4≤0时,即a≥-4时,
|5sin(θ+4)-a-4|≤|-5-a-4|=5+a+4=17
解得a=8≥-4,符合题意.
②当-a-4>0时,即a<-4时
|5sin(θ+4)-a-4|≤|5-a-4|=5-a-4=1-a=17
解得a=-16<-4,符合题意.
点评 本题主要考查曲线的参数方程、点到直线距离和三角函数的最值,难点在于如何根据曲线C上的点到直线l距离的最大值求出a.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)的一个周期为-2π | B. | y=f(x)的图象关于直线x=$\frac{8π}{3}$对称 | ||
| C. | f(x+π)的一个零点为x=$\frac{π}{6}$ | D. | f(x)在($\frac{π}{2}$,π)单调递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
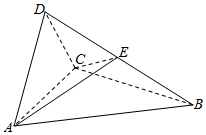 如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
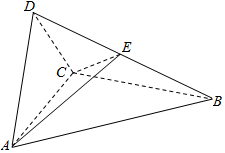 如图四面体ABCD中,△ABC是正三角形,AD=CD.
如图四面体ABCD中,△ABC是正三角形,AD=CD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com