
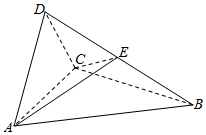
 如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD. 分析 (1)如图所示,取AC的中点O,连接BO,OD.△ABC是等边三角形,可得OB⊥AC.由已知可得:△ABD≌△CBD,AD=CD.△ACD是直角三角形,可得AC是斜边,∠ADC=90°.可得DO=$\frac{1}{2}$AC.利用DO2+BO2=AB2=BD2.可得OB⊥OD.利用线面面面垂直的判定与性质定理即可证明.
(2)设点D,B到平面ACE的距离分别为hD,hE.则$\frac{{h}_{D}}{{h}_{E}}$=$\frac{DE}{BE}$.根据平面AEC把四面体ABCD分成体积相等的两部分,可得$\frac{\frac{1}{3}{S}_{△ACE}•{h}_{D}}{\frac{1}{3}{S}_{△ACE}•{h}_{E}}$=$\frac{{h}_{D}}{{h}_{E}}$=$\frac{DE}{BE}$=1,即点E是BD的中点.建立如图所示的空间直角坐标系.不妨取AB=2.利用法向量的夹角公式即可得出.
解答 (1)证明:如图所示,取AC的中点O,连接BO,OD.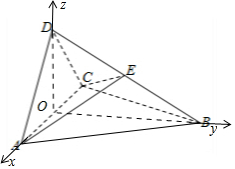
∵△ABC是等边三角形,∴OB⊥AC.
△ABD与△CBD中,AB=BD=BC,∠ABD=∠CBD,
∴△ABD≌△CBD,∴AD=CD.
∵△ACD是直角三角形,
∴AC是斜边,∴∠ADC=90°.
∴DO=$\frac{1}{2}$AC.
∴DO2+BO2=AB2=BD2.
∴∠BOD=90°.
∴OB⊥OD.
又DO∩AC=O,∴OB⊥平面ACD.
又OB?平面ABC,
∴平面ACD⊥平面ABC.
(2)解:设点D,B到平面ACE的距离分别为hD,hE.则$\frac{{h}_{D}}{{h}_{E}}$=$\frac{DE}{BE}$.
∵平面AEC把四面体ABCD分成体积相等的两部分,
∴$\frac{\frac{1}{3}{S}_{△ACE}•{h}_{D}}{\frac{1}{3}{S}_{△ACE}•{h}_{E}}$=$\frac{{h}_{D}}{{h}_{E}}$=$\frac{DE}{BE}$=1.
∴点E是BD的中点.
建立如图所示的空间直角坐标系.不妨取AB=2.
则O(0,0,0),A(1,0,0),C(-1,0,0),D(0,0,1),B(0,$\sqrt{3}$,0),E$(0,\frac{\sqrt{3}}{2},\frac{1}{2})$.
$\overrightarrow{AD}$=(-1,0,1),$\overrightarrow{AE}$=$(-1,\frac{\sqrt{3}}{2},\frac{1}{2})$,$\overrightarrow{AC}$=(-2,0,0).
设平面ADE的法向量为$\overrightarrow{m}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AD}=0}\\{\overrightarrow{m}•\overrightarrow{AE}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{-x+z=0}\\{-x+\frac{\sqrt{3}}{2}y+\frac{1}{2}z=0}\end{array}\right.$,取$\overrightarrow{m}$=$(3,\sqrt{3},3)$.
同理可得:平面ACE的法向量为$\overrightarrow{n}$=(0,1,$-\sqrt{3}$).
∴cos$<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{-2\sqrt{3}}{\sqrt{21}×2}$=-$\frac{\sqrt{7}}{7}$.
∴二面角D-AE-C的余弦值为$\frac{\sqrt{7}}{7}$.
点评 本题考查了空间位置关系、空间角、三棱锥的体积计算公式、向量夹角公式,考查了推理能力与计算能力,属于中档题.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:选择题
| A. | E(ξ1)<E(ξ2),D(ξ1)<D(ξ2) | B. | E(ξ1)<E(ξ2),D(ξ1)>D(ξ2) | C. | E(ξ1)>E(ξ2),D(ξ1)<D(ξ2) | D. | E(ξ1)>E(ξ2),D(ξ1)>D(ξ2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
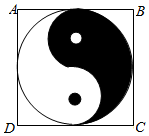 如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )
如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{π}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com