
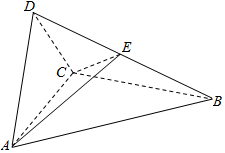
 如图四面体ABCD中,△ABC是正三角形,AD=CD.
如图四面体ABCD中,△ABC是正三角形,AD=CD.分析 (1)取AC中点O,连结DO、BO,推导出DO⊥AC,BO⊥AC,从而AC⊥平面BDO,由此能证明AC⊥BD.
(2)法一:连结OE,设AD=CD=$\sqrt{2}$,则OC=OA=1,由余弦定理求出BE=1,由BE=ED,四面体ABCE与四面体ACDE的高都是点A到平面BCD的高h,S△DCE=S△BCE,由此能求出四面体ABCE与四面体ACDE的体积比.法二:设AD=CD=$\sqrt{2}$,则AC=AB=BC=BD=2,AO=CO=DO=1,BO=$\sqrt{3}$,推导出BO⊥DO,以O为原点,OA为x轴,OB为y轴,OD为z轴,建立空间直角坐标系,由AE⊥EC,求出DE=BE,由此能求出四面体ABCE与四面体ACDE的体积比.
解答 证明:(1)取AC中点O,连结DO、BO,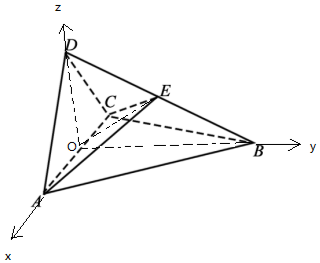
∵△ABC是正三角形,AD=CD,
∴DO⊥AC,BO⊥AC,
∵DO∩BO=O,∴AC⊥平面BDO,
∵BD?平面BDO,∴AC⊥BD.
解:(2)法一:连结OE,由(1)知AC⊥平面OBD,
∵OE?平面OBD,∴OE⊥AC,
设AD=CD=$\sqrt{2}$,则OC=OA=1,
∴E是线段AC垂直平分线上的点,∴EC=EA=CD=$\sqrt{2}$,
由余弦定理得:
cos∠CBD=$\frac{B{C}^{2}+B{D}^{2}-C{D}^{2}}{2BC•BD}$=$\frac{B{C}^{2}+B{E}^{2}-C{E}^{2}}{2BC•BE}$,
即$\frac{4+4-2}{2×2×2}=\frac{4+B{E}^{2}-2}{2×2×BE}$,解得BE=1或BE=2,
∵BE<<BD=2,∴BE=1,∴BE=ED,
∵四面体ABCE与四面体ACDE的高都是点A到平面BCD的高h,
∵BE=ED,∴S△DCE=S△BCE,
∴四面体ABCE与四面体ACDE的体积比为1.
法二:设AD=CD=$\sqrt{2}$,则AC=AB=BC=BD=2,AO=CO=DO=1,
∴BO=$\sqrt{4-1}$=$\sqrt{3}$,∴BO2+DO2=BD2,∴BO⊥DO,
以O为原点,OA为x轴,OB为y轴,OD为z轴,建立空间直角坐标系,
则C(-1,0,0),D(0,0,1),B(0,$\sqrt{3}$,0),A(1,0,0),
设E(a,b,c),$\overrightarrow{DE}=λ\overrightarrow{DB}$,(0≤λ≤1),则(a,b,c-1)=λ(0,$\sqrt{3}$,-1),解得E(0,$\sqrt{3}λ$,1-λ),
∴$\overrightarrow{CE}$=(1,$\sqrt{3}λ,1-λ$),$\overrightarrow{AE}$=(-1,$\sqrt{3}λ,1-λ$),
∵AE⊥EC,∴$\overrightarrow{AE}•\overrightarrow{CE}$=-1+3λ2+(1-λ)2=0,
由λ∈[0,1],解得$λ=\frac{1}{2}$,∴DE=BE,
∵四面体ABCE与四面体ACDE的高都是点A到平面BCD的高h,
∵DE=BE,∴S△DCE=S△BCE,
∴四面体ABCE与四面体ACDE的体积比为1.
点评 本题考查线线垂直的证明,考查两个四面体的体积之比的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、化归与转化思想,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
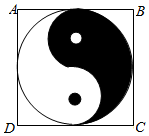 如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )
如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{π}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
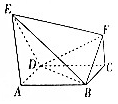 如图,正方形ABCD的边长为1,E,F是平面ABCD同一侧的两点,AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,FC=$\frac{1}{2}$.
如图,正方形ABCD的边长为1,E,F是平面ABCD同一侧的两点,AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,FC=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 440 | B. | 330 | C. | 220 | D. | 110 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com