
| A. | 440 | B. | 330 | C. | 220 | D. | 110 |
分析 方法一:由数列的性质,求得数列{bn}的通项公式及前n项和,可知当N为$\frac{n(n+1)}{2}$时(n∈N+),数列{an}的前N项和为数列{bn}的前n项和,即为2n+1-n-2,容易得到N>100时,n≥14,分别判断,即可求得该款软件的激活码;
方法二:由题意求得数列的每一项,及前n项和Sn=2n+1-2-n,及项数,由题意可知:2n+1为2的整数幂.只需将-2-n消去即可,分别即可求得N的值.
解答 解:设该数列为{an},设bn=${a}_{\frac{(n-1)n}{2}+1}$+…+${a}_{\frac{n(n+1)}{2}}$=2n+1-1,(n∈N+),则$\sum_{i=1}^{n}{b}_{i}$=$\sum_{i=1}^{\frac{n(n+1)}{2}}$ai,
由题意可设数列{an}的前N项和为SN,数列{bn}的前n项和为Tn,则Tn=21-1+22-1+…+2n+1-1=2n+1-n-2,
可知当N为$\frac{n(n+1)}{2}$时(n∈N+),数列{an}的前N项和为数列{bn}的前n项和,即为2n+1-n-2,
容易得到N>100时,n≥14,
A项,由$\frac{29×30}{2}$=435,440=435+5,可知S440=T29+b5=230-29-2+25-1=230,故A项符合题意.
B项,仿上可知$\frac{25×26}{2}$=325,可知S330=T25+b5=226-25-2+25-1=226+4,显然不为2的整数幂,故B项不符合题意.
C项,仿上可知$\frac{20×21}{2}$=210,可知S220=T20+b10=221-20-2+210-1=221+210-23,显然不为2的整数幂,故C项不符合题意.
D项,仿上可知$\frac{14×15}{2}$=105,可知S110=T14+b5=215-14-2+25-1=215+15,显然不为2的整数幂,故D项不符合题意.
故选A.
方法二:由题意可知:$\underset{\underbrace{{2}^{0}}}{第一项}$,$\frac{{2}^{0},{2}^{1}}{第二项}$,$\frac{{2}^{0},{2}^{1},{2}^{2}}{第三项}$,…$\frac{{2}^{0},{2}^{1},{2}^{2},…,{2}^{n-1}}{第n项}$,
根据等比数列前n项和公式,求得每项和分别为:21-1,22-1,23-1,…,2n-1,
每项含有的项数为:1,2,3,…,n,
总共的项数为N=1+2+3+…+n=$\frac{(1+n)n}{2}$,
所有项数的和为Sn:21-1+22-1+23-1+…+2n-1=(21+22+23+…+2n)-n=$\frac{2(1-{2}^{n})}{1-2}$-n=2n+1-2-n,
由题意可知:2n+1为2的整数幂.只需将-2-n消去即可,
则①1+2+(-2-n)=0,解得:n=1,总共有$\frac{(1+1)×1}{2}$+2=3,不满足N>100,
②1+2+4+(-2-n)=0,解得:n=5,总共有$\frac{(1+5)×5}{2}$+3=18,不满足N>100,
③1+2+4+8+(-2-n)=0,解得:n=13,总共有$\frac{(1+13)×13}{2}$+4=95,不满足N>100,
④1+2+4+8+16+(-2-n)=0,解得:n=29,总共有$\frac{(1+29)×29}{2}$+5=440,满足N>100,
∴该款软件的激活码440.
故选A.
点评 本题考查数列的应用,等差数列与等比数列的前n项和,考查计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
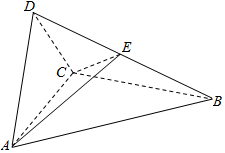 如图四面体ABCD中,△ABC是正三角形,AD=CD.
如图四面体ABCD中,△ABC是正三角形,AD=CD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
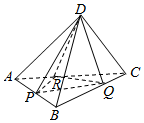 如图,已知正四面体D-ABC(所有棱长均相等的三棱锥),P、Q、R分别为AB、BC、CA上的点,AP=PB,$\frac{BQ}{QC}$=$\frac{CR}{RA}$=2,分别记二面角D-PR-Q,D-PQ-R,D-QR-P的平面角为α、β、γ,则( )
如图,已知正四面体D-ABC(所有棱长均相等的三棱锥),P、Q、R分别为AB、BC、CA上的点,AP=PB,$\frac{BQ}{QC}$=$\frac{CR}{RA}$=2,分别记二面角D-PR-Q,D-PQ-R,D-QR-P的平面角为α、β、γ,则( )| A. | γ<α<β | B. | α<γ<β | C. | α<β<γ | D. | β<γ<α |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
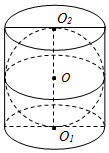 如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切,记圆柱O1O2的体积为V1,球O的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值是$\frac{3}{2}$.
如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切,记圆柱O1O2的体积为V1,球O的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值是$\frac{3}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
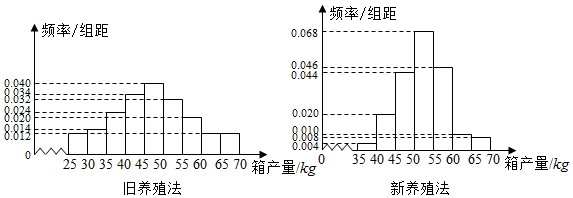
| 箱产量<50kg | 箱产量≥50kg | |
| 旧养殖法 | ||
| 新养殖法 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+$\frac{1}{b}$<$\frac{b}{{2}^{a}}$<log2(a+b)) | B. | $\frac{b}{{2}^{a}}$<log2(a+b)<a+$\frac{1}{b}$ | ||
| C. | a+$\frac{1}{b}$<log2(a+b)<$\frac{b}{{2}^{a}}$ | D. | log2(a+b))<a+$\frac{1}{b}$<$\frac{b}{{2}^{a}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com