
分析 由题意结合函数的单调性可得方程ax=x有两个不同实根m,n,转化为函数y=$\frac{lnx}{x}$与y=lna有两个不同交点,利用导数求得y=$\frac{lnx}{x}$的单调性及其最值,数形结合得答案.
解答 解:∵函数y=ax(a>1)为增函数,且其定义域与值域均为[m,n],
则am=m,an=n,即方程ax=x有两个不同实根m,n,
由ax=x,可知lnx=xlna,即$\frac{lnx}{x}=lna$,问题转化为函数y=$\frac{lnx}{x}$与y=lna有两个不同交点.
令y=$\frac{lnx}{x}$,则y′=$\frac{1-lnx}{{x}^{2}}$,
由y′=0,可得x=$\frac{1}{e}$,可知当x∈(0,e)时,y′>0,当x∈(e,+∞)时,y′<0.
∴y=$\frac{lnx}{x}$在(0,e)上单调递增,在(e,+∞)上单调递减.
结合图象可得0<lna<$\frac{1}{e}$,故1<a<${e}^{\frac{1}{e}}$.
故答案为:1<a<${e}^{\frac{1}{e}}$.
点评 本题考查函数的定义域及其值域,考查利用导数研究函数的单调性,体现了数学转化思想方法,是中档题.


科目:高中数学 来源: 题型:选择题
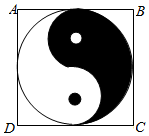 如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )
如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{π}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
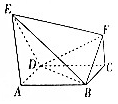 如图,正方形ABCD的边长为1,E,F是平面ABCD同一侧的两点,AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,FC=$\frac{1}{2}$.
如图,正方形ABCD的边长为1,E,F是平面ABCD同一侧的两点,AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,FC=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 随机变量ξ,η满足η=2ξ+3,则其方差的关系为D(η)=4D(ξ) | |
| B. | 回归分析中,R2的值越大,说明残差平方和越小 | |
| C. | 画残差图时,纵坐标一定为残差,横坐标一定为编号 | |
| D. | 回归直线一定过样本点中心 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 440 | B. | 330 | C. | 220 | D. | 110 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com