
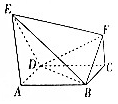
 如图,正方形ABCD的边长为1,E,F是平面ABCD同一侧的两点,AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,FC=$\frac{1}{2}$.
如图,正方形ABCD的边长为1,E,F是平面ABCD同一侧的两点,AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,FC=$\frac{1}{2}$.分析 (1)通过证明直线与平面两条相交直线垂直,然后证明直线与平面垂直.
(2)利用三棱锥的体积转化为几何体的体积减去两个三棱锥的体积即可.
解答 (1)证明:∵正方形ABCD的边长为1,∴CD∥AB,AB⊥AD,
∵AE⊥AB,AE∩AD=A,
∴AB⊥平面ADE,
∴CD⊥平面ADE.
(2)解:AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,可知:AE⊥底面ABCD,AC=$\sqrt{2}$,
FC=$\frac{1}{2}$.三棱锥E-BDF的体积:VEF-ABCD-VE-ABD-VF-BCD=$\frac{1}{3}×(\frac{AE+CF}{2})×AC×BD$$-\frac{1}{3}×\frac{1}{2}AD×AB×AE$$-\frac{1}{3}×\frac{1}{2}BC×DC×CF$
=$\frac{1}{3}×\frac{1+\frac{1}{2}}{2}×\sqrt{2}×\sqrt{2}$-$\frac{1}{3}×\frac{1}{2}×1×1×1$$-\frac{1}{3}×\frac{1}{2}×1×1×\frac{1}{2}$
=$\frac{1}{4}$.
点评 本题考查直线与平面垂直的判定定理的应用,几何体的体积的求法,考查计算能力以及转化思想的应用.


科目:高中数学 来源: 题型:解答题
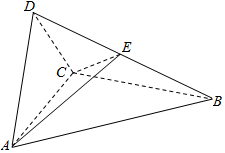 如图四面体ABCD中,△ABC是正三角形,AD=CD.
如图四面体ABCD中,△ABC是正三角形,AD=CD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{15}}{5}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°,E是PD的中点.
如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°,E是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
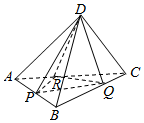 如图,已知正四面体D-ABC(所有棱长均相等的三棱锥),P、Q、R分别为AB、BC、CA上的点,AP=PB,$\frac{BQ}{QC}$=$\frac{CR}{RA}$=2,分别记二面角D-PR-Q,D-PQ-R,D-QR-P的平面角为α、β、γ,则( )
如图,已知正四面体D-ABC(所有棱长均相等的三棱锥),P、Q、R分别为AB、BC、CA上的点,AP=PB,$\frac{BQ}{QC}$=$\frac{CR}{RA}$=2,分别记二面角D-PR-Q,D-PQ-R,D-QR-P的平面角为α、β、γ,则( )| A. | γ<α<β | B. | α<γ<β | C. | α<β<γ | D. | β<γ<α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com