
分析 (1)利用数列的递推关系式,通过n≥2时,Sn-Sn-1=an,推出数列是等比数列,然后求解通项公式以及等差数列的通项公式即可.
(2)化简数列的通项公式,利用错位相减法求解数列的和即可.
解答 解;(1)∵∵Sn=2an-2,Sn-1=2an-1-2,$又{S_n}-{S_{n-1}}={a_n},(n≥2,n∈{N^*})$
∴an=2an-2an-1,∵an≠0,
∴$\frac{a_n}{{{a_{n-1}}}}=2,(n≥2,n∈{N^*}),即数列\left\{{a_n}\right\}是等比数列$.
$\begin{array}{l}∵{a_1}={S_1}$,∴${a_1}=2{a_1}-2,即{a_1}=2,\\∴{a_n}={2^n}\end{array}$
∴${a_n}={2^n}$,
∴bn+1-bn=2,即数列{bn}是等差数列,又b1=1,
∴bn=2n-1;
(2)∵∵${c_n}=(2n-1){2^n}$,
∴${T_n}={a_1}{b_1}+{a_2}{b_2}+…+{a_n}{b_n}=1×2+3×{2^2}+5×{2^3}+…+(2n-1){2^n}$,
∴2Tn=1×22+3×23+…+(2n-3)•2n+(2n-1)2n+1,
两式相减可得:
-Tn=1×2+2×22+2×23+…+2×2n-(2n-1)•2n+1
=2+2×$\frac{4(1-{2}^{n-1})}{1-2}$-(2n-1)•2n+1
=-6-(2n-3)•2n+1,
∴Tn=(2n-3)•2n+1+6.
点评 本题考查数列的递推关系式的应用,数列的通项公式以及数列求和,错位相减法求和的应用,考查计算能力.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
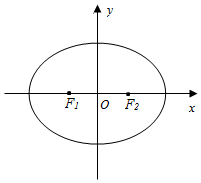 如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,离心率为$\frac{1}{2}$,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.
如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,离心率为$\frac{1}{2}$,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
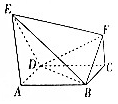 如图,正方形ABCD的边长为1,E,F是平面ABCD同一侧的两点,AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,FC=$\frac{1}{2}$.
如图,正方形ABCD的边长为1,E,F是平面ABCD同一侧的两点,AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,FC=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{{\sqrt{2}+1}}{2}}]$ | B. | $({-∞,\frac{{\sqrt{2}+1}}{2}}]$ | C. | (-∞,0] | D. | (-∞,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 随机变量ξ,η满足η=2ξ+3,则其方差的关系为D(η)=4D(ξ) | |
| B. | 回归分析中,R2的值越大,说明残差平方和越小 | |
| C. | 画残差图时,纵坐标一定为残差,横坐标一定为编号 | |
| D. | 回归直线一定过样本点中心 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com