
分析 (1)设等差数列{an}的公差为d,等比数列{bn}的公比为q,运用等差数列和等比数列的通项公式,列方程解方程可得d,q,即可得到所求通项公式;
(2)运用等比数列的求和公式,解方程可得公比,再由等差数列的通项公式和求和,计算即可得到所求和.
解答 解:(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q,
a1=-1,b1=1,a2+b2=2,a3+b3=5,
可得-1+d+q=2,-1+2d+q2=5,
解得d=1,q=2或d=3,q=0(舍去),
则{bn}的通项公式为bn=2n-1,n∈N*;
(2)b1=1,T3=21,
可得1+q+q2=21,
解得q=4或-5,
当q=4时,b2=4,a2=2-4=-2,
d=-2-(-1)=-1,S3=-1-2-3=-6;
当q=-5时,b2=-5,a2=2-(-5)=7,
d=7-(-1)=8,S3=-1+7+15=21.
点评 本题考查等差数列和等比数列的通项公式和求和公式的运用,求出公差和公比是解题的关键,考查方程思想和化简整理的运算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{7}{9}$ | B. | -$\frac{2}{9}$ | C. | $\frac{2}{9}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在区间[-$\frac{π}{6}$,$\frac{π}{3}$]上单调递减 | B. | 在区间[-$\frac{π}{6}$,$\frac{π}{3}$]上单调递增 | ||
| C. | 在区间[-$\frac{π}{3}$,$\frac{π}{6}$]上单调递减 | D. | 在区间[-$\frac{π}{3}$,$\frac{π}{6}$]上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
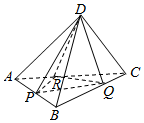 如图,已知正四面体D-ABC(所有棱长均相等的三棱锥),P、Q、R分别为AB、BC、CA上的点,AP=PB,$\frac{BQ}{QC}$=$\frac{CR}{RA}$=2,分别记二面角D-PR-Q,D-PQ-R,D-QR-P的平面角为α、β、γ,则( )
如图,已知正四面体D-ABC(所有棱长均相等的三棱锥),P、Q、R分别为AB、BC、CA上的点,AP=PB,$\frac{BQ}{QC}$=$\frac{CR}{RA}$=2,分别记二面角D-PR-Q,D-PQ-R,D-QR-P的平面角为α、β、γ,则( )| A. | γ<α<β | B. | α<γ<β | C. | α<β<γ | D. | β<γ<α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
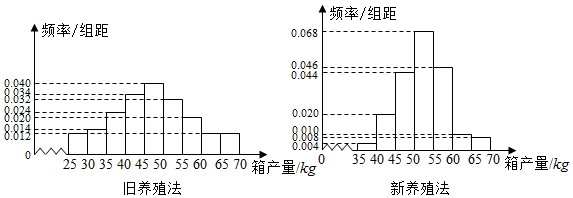
| 箱产量<50kg | 箱产量≥50kg | |
| 旧养殖法 | ||
| 新养殖法 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知{xn}是各项均为正数的等比数列,且x1+x2=3,x3-x2=2.
已知{xn}是各项均为正数的等比数列,且x1+x2=3,x3-x2=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com