
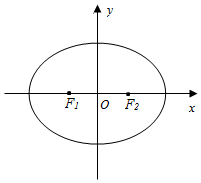
 ��ͼ����ƽ��ֱ������ϵxOy�У���ԲE��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ���ֱ�ΪF1��F2��������Ϊ$\frac{1}{2}$������֮��ľ���Ϊ8����P����ԲE�ϣ���λ�ڵ�һ���ޣ�����F1��ֱ��PF1�Ĵ���l1������F2��ֱ��PF2�Ĵ���l2��
��ͼ����ƽ��ֱ������ϵxOy�У���ԲE��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ���ֱ�ΪF1��F2��������Ϊ$\frac{1}{2}$������֮��ľ���Ϊ8����P����ԲE�ϣ���λ�ڵ�һ���ޣ�����F1��ֱ��PF1�Ĵ���l1������F2��ֱ��PF2�Ĵ���l2������ ��1������Բ�������ʹ�ʽ���a=2c������Բ���߷���x=��$\frac{2{a}^{2}}{c}$����2��$\frac{2{a}^{2}}{c}$=8���������a��c��ֵ����b2=a2-c2=3�����������Բ���̣�
��2����P�����꣬�ֱ����ֱ��PF2��б�ʼ�ֱ��PF1��б�ʣ������l2��l1��б�ʼ����̣��������Q�����꣬��Q����Բ���̣����y02=x02-1�������������P�����ꣻ
����������P��m��n������m��1ʱ��${k}_{P{F}_{2}}$=$\frac{n}{m-1}$��${k}_{P{F}_{1}}$=$\frac{n}{m+1}$�����ֱ��l1��l1�ķ��̣��������Q�����꣬���ݶԳ��Կɵ�$\frac{{m}^{2}-1}{n}$=��n2��������Բ���̣��������P�����꣮
��� �⣺��1���������֪����Բ��������e=$\frac{c}{a}$=$\frac{1}{2}$����a=2c����
��Բ���߷���x=��$\frac{{a}^{2}}{c}$����2��$\frac{{a}^{2}}{c}$=8����
�ɢ٢ڽ�ã�a=2��c=1��
��b2=a2-c2=3��
����Բ�ı����̣�$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$��
��2������һ����P��x0��y0������ֱ��PF2��б��${k}_{P{F}_{2}}$=$\frac{{y}_{0}}{{x}_{0}-1}$��
��ֱ��l2��б��k2=-$\frac{{x}_{0}-1}{{y}_{0}}$��ֱ��l2�ķ���y=-$\frac{{x}_{0}-1}{{y}_{0}}$��x-1����
ֱ��PF1��б��${k}_{P{F}_{1}}$=$\frac{{y}_{0}}{{x}_{0}+1}$��
��ֱ��l2��б��k1=-$\frac{{x}_{0}+1}{{y}_{0}}$��ֱ��l1�ķ���y=-$\frac{{x}_{0}+1}{{y}_{0}}$��x+1����
����$\left\{\begin{array}{l}{y=-\frac{{x}_{0}-1}{{y}_{0}}��x-1��}\\{y=-\frac{{x}_{0}+1}{{y}_{0}}��x+1��}\end{array}\right.$����ã�$\left\{\begin{array}{l}{x=-{x}_{0}}\\{y=\frac{{x}_{0}^{2}-1}{{y}_{0}}}\end{array}\right.$����Q��-x0��$\frac{{x}_{0}^{2}-1}{{y}_{0}}$����
��P��Q����Բ�ϣ�P��Q�ĺ����껥Ϊ�෴����������Ӧ��ȣ���y0=$\frac{{x}_{0}^{2}-1}{{y}_{0}}$��
��y02=x02-1��
��$\left\{\begin{array}{l}{\frac{{x}_{0}^{2}}{4}+\frac{{y}_{0}^{2}}{3}=1}\\{{y}_{0}^{2}={x}_{0}^{2}-1}\end{array}\right.$����ã�$\left\{\begin{array}{l}{{x}_{0}^{2}=\frac{16}{7}}\\{{y}_{0}^{2}=\frac{9}{7}}\end{array}\right.$����$\left\{\begin{array}{l}{{x}_{0}=��\frac{4\sqrt{7}}{7}}\\{{y}_{0}=��\frac{3\sqrt{7}}{7}}\end{array}\right.$��
��P�ڵ�һ���ޣ�����P������Ϊ��
P��$\frac{4\sqrt{7}}{7}$��$\frac{3\sqrt{7}}{7}$����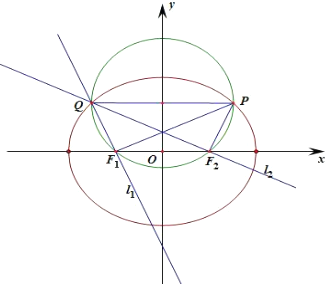
����������P��m��n������P�ڵ�һ���ޣ���m��0��n��0��
��m=1ʱ��${k}_{P{F}_{2}}$�����ڣ���ã�Q��F1�غϣ����������⣬
��m��1ʱ��${k}_{P{F}_{2}}$=$\frac{n}{m-1}$��${k}_{P{F}_{1}}$=$\frac{n}{m+1}$��
��l1��PF1��l2��PF2����${k}_{{l}_{1}}$=-$\frac{m+1}{n}$��${k}_{{l}_{2}}$=-$\frac{m-1}{n}$��
ֱ��l1�ķ���y=-$\frac{m+1}{n}$��x+1������ֱ��l2�ķ���y=-$\frac{m-1}{n}$��x-1������
������ã�x=-m����Q��-m��$\frac{{m}^{2}-1}{n}$����
��Q����Բ���̣��ɶԳ��Կɵã�$\frac{{m}^{2}-1}{n}$=��n2��
��m2-n2=1����m2+n2=1��
��P��m��n��������Բ���̣�$\left\{\begin{array}{l}{{m}^{2}-1={n}^{2}}\\{\frac{{m}^{2}}{4}+\frac{{n}^{2}}{3}=1}\end{array}\right.$����ã�$\left\{\begin{array}{l}{{m}^{2}=\frac{16}{7}}\\{{n}^{2}=\frac{9}{7}}\end{array}\right.$����$\left\{\begin{array}{l}{1-{m}^{2}={n}^{2}}\\{\frac{{m}^{2}}{4}+\frac{{n}^{2}}{3}=1}\end{array}\right.$���⣬
��P�ڵ�һ���ޣ�����P������Ϊ��
P��$\frac{4\sqrt{7}}{7}$��$\frac{3\sqrt{7}}{7}$����
���� ���⿼����Բ�ı����̣�ֱ������Բ��λ�ù�ϵ������ֱ�ߵ�б�ʹ�ʽ���������ν��˼�룬������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����еĸ���������ʱ���ü�������� | |
| B�� | ϵͳ���������У���������ֺ��ÿһ�����г�ȡһ�����壬�õ��������� | |
| C�� | �ٻ��̳���ץ����dz�ǩ�� | |
| D�� | �������������У�ÿ�����屻��ȡ�ĸ�����ȣ�����ʱ���⣩ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��x����һ������Ϊ-2�� | B�� | y=f��x����ͼ�����ֱ��x=$\frac{8��}{3}$�Գ� | ||
| C�� | f��x+�У���һ�����Ϊx=$\frac{��}{6}$ | D�� | f��x���ڣ�$\frac{��}{2}$���У������ݼ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
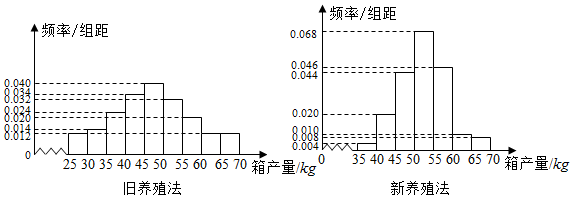
| �������50kg | �������50kg | |
| ����ֳ�� | ||
| ����ֳ�� |
| P��K2��K�� | 0.050 | 0.010 | 0.001 |
| K | 3.841 | 6.635 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
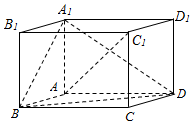 ��ͼ����ƽ��������ABCD-A1B1C1D1�У�AA1��ƽ��ABCD����AB=AD=2��AA1=$\sqrt{3}$����BAD=120�㣮
��ͼ����ƽ��������ABCD-A1B1C1D1�У�AA1��ƽ��ABCD����AB=AD=2��AA1=$\sqrt{3}$����BAD=120�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��C1�ϸ���ĺ������쳤��ԭ����2���������겻�䣬�ٰѵõ�����������ƽ��$\frac{��}{6}$����λ���ȣ��õ�����C2 | |
| B�� | ��C1�ϸ���ĺ������쳤��ԭ����2���������겻�䣬�ٰѵõ�����������ƽ��$\frac{��}{12}$����λ���ȣ��õ�����C2 | |
| C�� | ��C1�ϸ���ĺ��������̵�ԭ����$\frac{1}{2}$���������겻�䣬�ٰѵõ�����������ƽ��$\frac{��}{6}$����λ���ȣ��õ�����C2 | |
| D�� | ��C1�ϸ���ĺ��������̵�ԭ����$\frac{1}{2}$���������겻�䣬�ٰѵõ�����������ƽ��$\frac{��}{12}$����λ���ȣ��õ�����C2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{7}{9}$ | B�� | -$\frac{2}{9}$ | C�� | $\frac{2}{9}$ | D�� | $\frac{7}{9}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com