练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．下列说法中错误的是（　　）
    A．总体中的个体数不多时宜用简单随机抽样
    B．系统抽样过程中，在总体均分后的每一部分中抽取一个个体，得到所需样本
    C．百货商场的抓奖活动是抽签法
    D．整个抽样过程中，每个个体被抽取的概率相等（有剔除时例外）

    分析 利用简单随机抽样、系统抽样的概念对A、B、C、D四个选项逐一分析即可得到答案．

    解答 解：对于A，当总体中的个体数不多时宜用简单随机抽样，正确；
    对于B，系统抽样过程中，在总体均分后的每一部分中抽取一个个体，得到所需样本，正确；
    对于C，百货商场的抓奖活动是抽签法，正确；
    对于D，整个抽样过程中，每个个体被抽取的概率相等（包括有剔除时），故“有剔除时例外”的说法错误；
    故选：D．

    点评 本题考查命题的真假判断与应用，突出考查简单随机抽样、系统抽样的概念及应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    13．已知集合A={x|x＜2}，B={x|3-2x＞0}，则（　　）
    A．A∩B={x|x＜$\frac{3}{2}$}B．A∩B=∅C．A∪B={x|x＜$\frac{3}{2}$}D．AUB=R

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{9}=1$（a＞0）的一条渐近线方程为y=$\frac{3}{5}$x，则a=5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

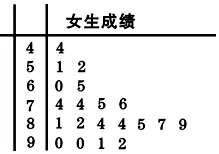    11．为了研究某学科成绩（满分100分）是否与学生性别有关，采用分层抽样的方法，从高二年级抽取了30名男生和20名女生的该学科成绩，得到如图所示女生成绩的茎叶图．其中抽取的男生中有21人的成绩在80分以下，规定80分以上为优秀（含80分）．
    （1）请根据题意，将2×2列联表补充完整；
    优秀非优秀总计
    男生
    女生
    总计50
    （2）据此列联表判断，是否有90%的把握认为该学科成绩与性别有关？
    附：x2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
    参考数据当x2≤2.706时，无充分证据判定变量A，B有关联，可以认为两变量无关联；
    当x2＞2.706时，有90%的把握判定变量A，B有关联；
    当x2＞3.841时，有95%的把握判定变量A，B有关联；
    当x2＞6.635时，有99%的把握判定变量A，B有关联．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知复数z满足z（1+i）=2i，则z的共轭复数$\overline{z}$等于（　　）
    A．1+iB．1-iC．-1+iD．-1-i

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．下面是关于复数z=2-i的四个命题：p1：|z|=5；p2：z2=3-4i；p3：z的共轭复数为-2+i；p4：z的虚部为-1，其中真命题为（　　）
    A．p2，p3B．p1，p2C．p2，p4D．p3，p4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．给出下列三个命题：
    ①若回归直线的斜率估计值是1.23，样本点的中心为（4，5），则回归直线方程是$\widehaty=1.23x+0.08$；
    ②若偶函数f（x）（x∈R）满足f（x+1）=-f（x），且x∈[0，1]时，f（x）=x，则方程f（x）=log3|x|有3个根；
    ③已知函数f（x）=（$\frac{3}{2}$）x-sinx-1在[0，+∞）内只有两个零点．
    正确命题的序号是①③（把你认为正确命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．设A，B是椭圆C：$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{m}$=1长轴的两个端点，若C上存在点M满足∠AMB=120°，则m的取值范围是（　　）
    A．（0，1]∪[9，+∞）B．（0，$\sqrt{3}$]∪[9，+∞）C．（0，1]∪[4，+∞）D．（0，$\sqrt{3}$]∪[4，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

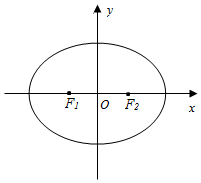    13．如图，在平面直角坐标系xOy中，椭圆E：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F1，F2，离心率为$\frac{1}{2}$，两准线之间的距离为8．点P在椭圆E上，且位于第一象限，过点F1作直线PF1的垂线l1，过点F2作直线PF2的垂线l2．
    （1）求椭圆E的标准方程；
    （2）若直线l1，l2的交点Q在椭圆E上，求点P的坐标．

    查看答案和解析>>

    同步练习册答案