Question

15．给出下列三个命题：
①若回归直线的斜率估计值是1.23，样本点的中心为（4，5），则回归直线方程是$\widehaty=1.23x+0.08$；
②若偶函数f（x）（x∈R）满足f（x+1）=-f（x），且x∈[0，1]时，f（x）=x，则方程f（x）=log₃|x|有3个根；
③已知函数f（x）=（$\frac{3}{2}$）^x-sinx-1在[0，+∞）内只有两个零点．
正确命题的序号是①③（把你认为正确命题的序号都填上）

Answer 1

分析 求出回归系数，进而得到回归直线方程，可判断①；
分析函数y=f（x）与y=log₃|x|的图象交点的个数，可判断②；
分析函数y=（$\frac{3}{2}$）^x与y=sinx+1的图象在[0，+∞）内交点的个数，可判断③．

解答 解：①若回归直线的斜率估计值是1.23，样本点的中心为（4，5），
则$\hat{a}$=5-4×1.23=0.08，故回归直线方程是$\widehaty=1.23x+0.08$，故正确；
②若偶函数f（x）（x∈R）满足f（x+1）=-f（x），则函数周期为2，
且x∈[0，1]时，f（x）=x，
则函数y=f（x）与y=log₃|x|的图象在（0，+∞）上有两个交点，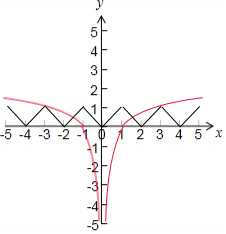

即函数y=f（x）与y=log₃|x|的图象有四个交点，
则方程f（x）=log₃|x|有4个根，故错误；
③由函数y=（$\frac{3}{2}$）^x与y=sinx+1的图象在[0，+∞）内只有两个交点．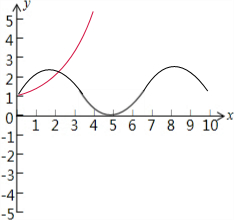

故函数f（x）=（$\frac{3}{2}$）^x-sinx-1在[0，+∞）内只有两个零点，故正确．
故答案为：①③

点评 本题以命题的真假判断与应用为载体考查了函数的零点，回归直线方程，难度中档．