
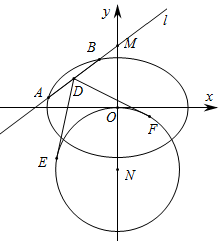
 在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,椭圆C截直线y=1所得线段的长度为2$\sqrt{2}$.
在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,椭圆C截直线y=1所得线段的长度为2$\sqrt{2}$.分析 (Ⅰ)首先根据题中信息可得椭圆C过点($\sqrt{2}$,1),然后结合离心率可得椭圆方程;
(Ⅱ)可将题目所求角度的最小值转化为求角度正弦的最小值,结合题目信息可求得D、N坐标及⊙N半径,进而将DN长度表示出来,可求∠EDF最小值.
解答 解:(Ⅰ)∵椭圆C的离心率为$\frac{\sqrt{2}}{2}$,
∴$\frac{{a}^{2}-{b}^{2}}{{a}^{2}}$=$\frac{1}{2}$,a2=2b2,
∵椭圆C截直线y=1所得线段的长度为2$\sqrt{2}$,
∴椭圆C过点($\sqrt{2}$,1),
∴$\frac{2}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=1,
∴b2=2,a2=4,
∴椭圆C的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1.
(Ⅱ)设A,B的横坐标为x1,x2,
则A(x1,kx1+m),B(x2,kx2+m),D($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{k}{2}({x}_{1}+{x}_{2})$+m),
联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\\{y=kx+m}\end{array}\right.$可得(1+2k2)x2+4kmx+2m2-4=0,
∴x1+x2=-$\frac{4km}{1+2{k}^{2}}$,
∴D(-$\frac{2km}{1+2{k}^{2}}$,$\frac{m}{1+2{k}^{2}}$),
∵M(0,m),则N(0,-m),
∴⊙N的半径为|m|,
|DN|=$\sqrt{(\frac{m}{1+2{k}^{2}}+m)^{2}+(\frac{-2km}{1+2{k}^{2}})^{2}}$=$\frac{|2m|}{1+2{k}^{2}}$$\sqrt{{k}^{4}+3{k}^{2}+1}$,
设∠EDF=α,
∴sin$\frac{α}{2}$=$\frac{EN}{DN}$=$\frac{ON}{DN}$=$\frac{m}{\frac{2m}{1+2{k}^{2}}\sqrt{{k}^{4}+3{k}^{2}+1}}$=$\frac{1+2{k}^{2}}{2\sqrt{{k}^{4}+3{k}^{2}+1}}$,
令y=$\frac{1+2{k}^{2}}{2\sqrt{{k}^{4}+3{k}^{2}+1}}$,则y′=$\frac{1}{2}$$\frac{k(4{k}^{2}+1)}{\sqrt{{k}^{4}+3{k}^{2}+1}({k}^{4}+3{k}^{2}+1)}$,
当k=0时,sin$\frac{α}{2}$取得最小值,最小值为$\frac{1}{2}$.
∴∠EDF的最小值是60°.
点评 本题考查圆锥曲线的最值问题,重要的是能将角度的最小值进行转化求解.


科目:高中数学 来源: 题型:解答题
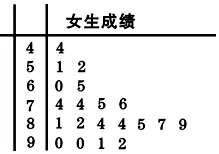 为了研究某学科成绩(满分100分)是否与学生性别有关,采用分层抽样的方法,从高二年级抽取了30名男生和20名女生的该学科成绩,得到如图所示女生成绩的茎叶图.其中抽取的男生中有21人的成绩在80分以下,规定80分以上为优秀(含80分).
为了研究某学科成绩(满分100分)是否与学生性别有关,采用分层抽样的方法,从高二年级抽取了30名男生和20名女生的该学科成绩,得到如图所示女生成绩的茎叶图.其中抽取的男生中有21人的成绩在80分以下,规定80分以上为优秀(含80分).| 优秀 | 非优秀 | 总计 | |
| 男生 | |||
| 女生 | |||
| 总计 | 50 |
| 参考数据 | 当x2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当x2>2.706时,有90%的把握判定变量A,B有关联; | |
| 当x2>3.841时,有95%的把握判定变量A,B有关联; | |
| 当x2>6.635时,有99%的把握判定变量A,B有关联. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p2,p3 | B. | p1,p2 | C. | p2,p4 | D. | p3,p4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1]∪[9,+∞) | B. | (0,$\sqrt{3}$]∪[9,+∞) | C. | (0,1]∪[4,+∞) | D. | (0,$\sqrt{3}$]∪[4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
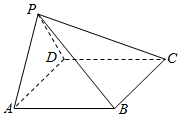 如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.
如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com