
| A�� | ��C1�ϸ���ĺ������쳤��ԭ����2���������겻�䣬�ٰѵõ�����������ƽ��$\frac{��}{6}$����λ���ȣ��õ�����C2 | |
| B�� | ��C1�ϸ���ĺ������쳤��ԭ����2���������겻�䣬�ٰѵõ�����������ƽ��$\frac{��}{12}$����λ���ȣ��õ�����C2 | |
| C�� | ��C1�ϸ���ĺ��������̵�ԭ����$\frac{1}{2}$���������겻�䣬�ٰѵõ�����������ƽ��$\frac{��}{6}$����λ���ȣ��õ�����C2 | |
| D�� | ��C1�ϸ���ĺ��������̵�ԭ����$\frac{1}{2}$���������겻�䣬�ٰѵõ�����������ƽ��$\frac{��}{12}$����λ���ȣ��õ�����C2 |
���� �������Ǻ����������任�Լ�ƽ�Ʊ任ת����⼴�ɣ�
��� �⣺��C1�ϸ���ĺ��������̵�ԭ����$\frac{1}{2}$���������겻�䣬�õ�����y=cos2xͼ���ٰѵõ�����������ƽ��$\frac{��}{12}$����λ���ȣ��õ�����y=cos2��x+$\frac{��}{12}$��=cos��2x+$\frac{��}{6}$��=sin��2x+$\frac{2��}{3}$����ͼ������C2��
��ѡ��D��
���� ���⿼�����Ǻ�����ͼ��任���յ���ʽ��Ӧ�ã��������������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4�� | B�� | 2�� | C�� | �� | D�� | $\frac{��}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
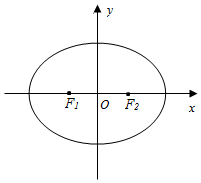 ��ͼ����ƽ��ֱ������ϵxOy�У���ԲE��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ���ֱ�ΪF1��F2��������Ϊ$\frac{1}{2}$������֮��ľ���Ϊ8����P����ԲE�ϣ���λ�ڵ�һ���ޣ�����F1��ֱ��PF1�Ĵ���l1������F2��ֱ��PF2�Ĵ���l2��
��ͼ����ƽ��ֱ������ϵxOy�У���ԲE��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ���ֱ�ΪF1��F2��������Ϊ$\frac{1}{2}$������֮��ľ���Ϊ8����P����ԲE�ϣ���λ�ڵ�һ���ޣ�����F1��ֱ��PF1�Ĵ���l1������F2��ֱ��PF2�Ĵ���l2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
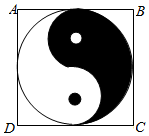 ��ͼ��������ABCD�ڵ�ͼ�������й��Ŵ���̫��ͼ������������Բ�еĺ�ɫ���ֺͰ�ɫ���ֹ��������ε����ij����ĶԳƣ��������������ȡһ�㣬��˵�ȡ�Ժ�ɫ���ֵĸ����ǣ�������
��ͼ��������ABCD�ڵ�ͼ�������й��Ŵ���̫��ͼ������������Բ�еĺ�ɫ���ֺͰ�ɫ���ֹ��������ε����ij����ĶԳƣ��������������ȡһ�㣬��˵�ȡ�Ժ�ɫ���ֵĸ����ǣ�������| A�� | $\frac{1}{4}$ | B�� | $\frac{��}{8}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{��}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
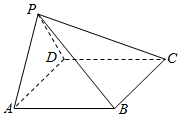 ��ͼ��������P-ABCD�У�AB��CD���ҡ�BAP=��CDP=90�㣮
��ͼ��������P-ABCD�У�AB��CD���ҡ�BAP=��CDP=90�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��������Σ��������=2��+3�����䷽��Ĺ�ϵΪD���ǣ�=4D���Σ� | |
| B�� | �ع�����У�R2��ֵԽ��˵���в�ƽ����ԽС | |
| C�� | ���в�ͼʱ��������һ��Ϊ�в������һ��Ϊ��� | |
| D�� | �ع�ֱ��һ�������������� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com