
分析 (1)求导,根据导数与函数单调性的关系,分类讨论,即可求得f(x)单调性;
(2)由(1)可知:当a>0时才有两个零点,根据函数的单调性求得f(x)最小值,由f(x)min<0,g(a)=alna+a-1,a>0,求导,由g(a)min=g(e-2)=e-2lne-2+e-2-1=-$\frac{1}{{e}^{2}}$-1,g(1)=0,即可求得a的取值范围.
(1)求导,根据导数与函数单调性的关系,分类讨论,即可求得f(x)单调性;
(2)分类讨论,根据函数的单调性及函数零点的判断,分别求得函数的零点,即可求得a的取值范围.
解答 解:(1)由f(x)=ae2x+(a-2)ex-x,求导f′(x)=2ae2x+(a-2)ex-1,
当a=0时,f′(x)=-2ex-1<0,
∴当x∈R,f(x)单调递减,
当a>0时,f′(x)=(2ex+1)(aex-1)=2a(ex+$\frac{1}{2}$)(ex-$\frac{1}{a}$),
令f′(x)=0,解得:x=ln$\frac{1}{a}$,
当f′(x)>0,解得:x>ln$\frac{1}{a}$,
当f′(x)<0,解得:x<ln$\frac{1}{a}$,
∴x∈(-∞,ln$\frac{1}{a}$)时,f(x)单调递减,x∈(ln$\frac{1}{a}$,+∞)单调递增;
当a<0时,f′(x)=2a(ex+$\frac{1}{2}$)(ex-$\frac{1}{a}$)<0,恒成立,
∴当x∈R,f(x)单调递减,
综上可知:当a≤0时,f(x)在R单调减函数,
当a>0时,f(x)在(-∞,ln$\frac{1}{a}$)是减函数,在(ln$\frac{1}{a}$,+∞)是增函数;
(2)①若a≤0时,由(1)可知:f(x)最多有一个零点,
当a>0时,f(x)=ae2x+(a-2)ex-x,
当x→-∞时,e2x→0,ex→0,
∴当x→-∞时,f(x)→+∞,
当x→∞,e2x→+∞,且远远大于ex和x,
∴当x→∞,f(x)→+∞,
∴函数有两个零点,f(x)的最小值小于0即可,
由f(x)在(-∞,ln$\frac{1}{a}$)是减函数,在(ln$\frac{1}{a}$,+∞)是增函数,
∴f(x)min=f(ln$\frac{1}{a}$)=a×($\frac{1}{{a}^{2}}$)+(a-2)×$\frac{1}{a}$-ln$\frac{1}{a}$<0,
∴1-$\frac{1}{a}$-ln$\frac{1}{a}$<0,即ln$\frac{1}{a}$+$\frac{1}{a}$-1>0,
设t=$\frac{1}{a}$,则g(t)=lnt+t-1,(t>0),
求导g′(t)=$\frac{1}{t}$+1,由g(1)=0,
∴t=$\frac{1}{a}$>1,解得:0<a<1,
∴a的取值范围(0,1).
方法二:(1)由f(x)=ae2x+(a-2)ex-x,求导f′(x)=2ae2x+(a-2)ex-1,
当a=0时,f′(x)=2ex-1<0,
∴当x∈R,f(x)单调递减,
当a>0时,f′(x)=(2ex+1)(aex-1)=2a(ex+$\frac{1}{2}$)(ex-$\frac{1}{a}$),
令f′(x)=0,解得:x=-lna,
当f′(x)>0,解得:x>-lna,
当f′(x)<0,解得:x<-lna,
∴x∈(-∞,-lna)时,f(x)单调递减,x∈(-lna,+∞)单调递增;
当a<0时,f′(x)=2a(ex+$\frac{1}{2}$)(ex-$\frac{1}{a}$)<0,恒成立,
∴当x∈R,f(x)单调递减,
综上可知:当a≤0时,f(x)在R单调减函数,
当a>0时,f(x)在(-∞,-lna)是减函数,在(-lna,+∞)是增函数;
(2)①若a≤0时,由(1)可知:f(x)最多有一个零点,
②当a>0时,由(1)可知:当x=-lna时,f(x)取得最小值,f(x)min=f(-lna)=1-$\frac{1}{a}$-ln$\frac{1}{a}$,
当a=1,时,f(-lna)=0,故f(x)只有一个零点,
当a∈(1,+∞)时,由1-$\frac{1}{a}$-ln$\frac{1}{a}$>0,即f(-lna)>0,
故f(x)没有零点,
当a∈(0,1)时,1-$\frac{1}{a}$-ln$\frac{1}{a}$<0,f(-lna)<0,
由f(-2)=ae-4+(a-2)e-2+2>-2e-2+2>0,
故f(x)在(-∞,-lna)有一个零点,
假设存在正整数n0,满足n0>ln($\frac{3}{a}$-1),则f(n0)=${e}^{{n}_{0}}$(a${e}^{{n}_{0}}$+a-2)-n0>${e}^{{n}_{0}}$-n0>${2}^{{n}_{0}}$-n0>0,
由ln($\frac{3}{a}$-1)>-lna,
因此在(-lna,+∞)有一个零点.
∴a的取值范围(0,1).
点评 本题考查导数的综合应用,考查利用导数求函数单调性及最值,考查函数零点的判断,考查计算能力,考查分类讨论思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | E(ξ1)<E(ξ2),D(ξ1)<D(ξ2) | B. | E(ξ1)<E(ξ2),D(ξ1)>D(ξ2) | C. | E(ξ1)>E(ξ2),D(ξ1)<D(ξ2) | D. | E(ξ1)>E(ξ2),D(ξ1)>D(ξ2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
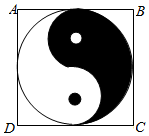 如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )
如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{π}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com