Question

6．已知两点A（1，0），B（1，$\sqrt{3}$），O为坐标原点，点C在第二象限，且∠AOC=120°，设$\overrightarrow{OC}$=-2$\overrightarrow{OA}$+λ$\overrightarrow{OB}$（λ∈R）则λ=1．

Answer 1

分析 设|OC|=c，根据已知条件即可表示出C点坐标为（$-\frac{1}{2}c，\frac{\sqrt{3}}{2}c$），进行向量的坐标运算从而可得到$（-\frac{1}{2}c，\frac{\sqrt{3}}{2}c）=（λ-2，\sqrt{3}λ）$，这便能得到$\left\{\begin{array}{l}{-\frac{1}{2}c=λ-2}\\{\frac{\sqrt{3}}{2}c=\sqrt{3}λ}\end{array}\right.$，解方程组即可得到λ的值．

解答 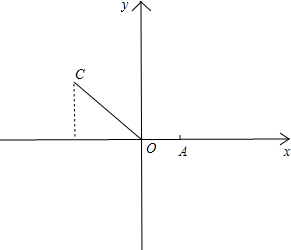解：如图，
设|OC|=c，根据∠AOC=120°；
∴$C（-\frac{1}{2}c，\frac{\sqrt{3}}{2}c）$；
∴由$\overrightarrow{OC}=-2\overrightarrow{OA}+λ\overrightarrow{OB}$及A，B点坐标得：
（$-\frac{1}{2}c，\frac{\sqrt{3}}{2}c$）=-2（1，0）+$λ（1，\sqrt{3}）$；
∴$\left\{\begin{array}{l}{-\frac{1}{2}c=λ-2}\\{\frac{\sqrt{3}}{2}c=\sqrt{3}λ}\end{array}\right.$；
解得λ=1．
故答案为：1．

点评 考查由三角函数的定义表示点的坐标，向量坐标和点的坐标的关系，以及向量的坐标运算，解二元一次方程组．