
分析 先根据定积分的几何意义,将原式化成${∫}_{0}^{1}$(1-x2)dx+${∫}_{1}^{3}$(x2-1)dx,再利用定积分的运算法则,找出被积函数的原函数,进行计算即可.
解答 解:由题意可知:$\int_{0}^{3}{|{x^2}-1|}dx$=${∫}_{0}^{1}$(1-x2)dx+${∫}_{1}^{3}$(x2-1)dx,
=(x-$\frac{1}{3}$x3)${丨}_{0}^{1}$+($\frac{1}{3}$x3-x)${丨}_{1}^{3}$,
=(1-$\frac{1}{3}$)+(9-3)+($\frac{1}{3}$-1),
=$\frac{22}{3}$,
故答案为:$\frac{22}{3}$.
点评 本题主要考查定积分的基本运算,解题关键是找出被积函数的原函数,利用区间去绝对值符号也是注意点,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
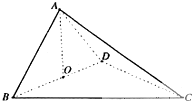 如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,AB=2,AC=$\sqrt{6}$.
如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,AB=2,AC=$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com