
 某英语学习小组共12名同学进行英语听力测试,随机抽取6名同学的测试成绩(单位:分),用茎叶图记录如下,其中茎为十位数,叶为个位数.
某英语学习小组共12名同学进行英语听力测试,随机抽取6名同学的测试成绩(单位:分),用茎叶图记录如下,其中茎为十位数,叶为个位数.. |
| x |
| x1+x2+x3+…+xn |
| n |
| 2 |
| 6 |
| C | 2 12 |
| C | 1 10 |
| C | 1 2 |
. |
| x |
| 18+19+21+22+28+30 |
| 6 |
| 2 |
| 6 |
| C | 2 12 |
| C | 1 10 |
| C | 1 2 |
| ||||
|
| 20 |
| 66 |
| 10 |
| 33 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 1 |
| anan+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| n |
| an |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
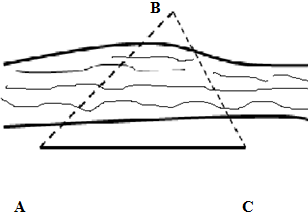 如图,在一次测量活动中,要测量河两岸B、C两点间的距离,测量者在河的一侧,测得AC=24m,∠BAC=45°,∠ACB=75°,求B、C两点间的距离.
如图,在一次测量活动中,要测量河两岸B、C两点间的距离,测量者在河的一侧,测得AC=24m,∠BAC=45°,∠ACB=75°,求B、C两点间的距离.查看答案和解析>>
科目:高中数学 来源: 题型:
| 1+ln(x-1) |
| x-a |
| m |
| x |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| n |
| n+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com