
分析 (1)利用三角函数恒等变换的应用化简已知等式可得:2sinAcosA=-sinA,由于sinA≠0,解得cosA=-$\frac{1}{2}$,从而可求A的值.
(2)由正弦定理化简已知等式可得3b=4c,利用三角形面积公式结合已知可解得bc=12,联立可解得b,c的值,利用余弦定理即可求得a的值.
解答 解:(1)∵sin2A+2sinCcosB=sin(C-B),
∴2sinAcosA+2sinCcosB=sinCcosB-cosCsinB,整理可得:2sinAcosA=-(cosCsinB+sinCcosB)=-sin(B+C)=-sinA,
∵A∈(0,π),sinA≠0,
∴解得:cosA=-$\frac{1}{2}$,A=$\frac{2π}{3}$.
(2)∵3sinB=4sinC,
∴由正弦定理可得:3b=4c,①
∵S△ABC=3$\sqrt{3}$=$\frac{1}{2}$bcsinA=$\frac{1}{2}×\frac{\sqrt{3}}{2}$bc,解得:bc=12,②
∴由①②可解得:b=4,c=3,
∴由余弦定理可得:a=$\sqrt{{b}^{2}+{c}^{2}-2bccosA}$=$\sqrt{16+9-2×4×3×(-\frac{1}{2})}$=$\sqrt{37}$.
点评 本题主要考查了三角函数恒等变换的应用,正弦定理,三角形面积公式,余弦定理在解三角形中的应用,考查了计算能力和转化思想,属于中档题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
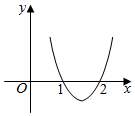 已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导导数y=f′(x)的图象经过点(1,0),(2,0),如图所示,求x0的值和函数(x)的极小值.
已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导导数y=f′(x)的图象经过点(1,0),(2,0),如图所示,求x0的值和函数(x)的极小值.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com