
���� ��I�����õ��ƹ�ϵ��Ȳ����еĶ��弴��֤����
��II�����á���λ���������ȱ����е�ǰn���ʽ���ɵó���
��� ��I��֤������$\frac{{2S}_{n}}{n}$=an+1-$\frac{1}{3}$n2-n-$\frac{2}{3}$��n��N*����2Sn=nan+1-$\frac{1}{3}{n}^{3}$-n2-$\frac{2}{3}n$��
��n��2ʱ��2Sn-1=��n-1��an-$\frac{1}{3}��n-1��^{3}$-��n-1��2-$\frac{2}{3}$��n-1����
�ɵã�2an=nan+1-��n-1��an-n��n+1����
��Ϊ$\frac{{a}_{n+1}}{n+1}$-$\frac{{a}_{n}}{n}$=1��
��{$\frac{{a}_{n}}{n}$}Ϊ�Ȳ����У�����Ϊ1������Ϊ1��
�ɵ�$\frac{{a}_{n}}{n}$=1+��n-1��=n�����an=n2��
��II���⣺cn=$\frac{\sqrt{{a}_{n}}-2}{{2}^{n-1}}$=$\frac{n-2}{{2}^{n-1}}$��
������{cn}��ǰn���ΪTn=-1+0+$\frac{1}{{2}^{2}}$+$\frac{2}{{2}^{3}}$+��+$\frac{n-2}{{2}^{n-1}}$��
$\frac{1}{2}{T}_{n}$=$-\frac{1}{2}$+0+$\frac{1}{{2}^{3}}$+��+$\frac{n-3}{{2}^{n-1}}$+$\frac{n-2}{{2}^{n}}$��
��$\frac{1}{2}{T}_{n}$=-1+$\frac{1}{2}+\frac{1}{{2}^{2}}$+��+$\frac{1}{{2}^{n-1}}$-$\frac{n-2}{{2}^{n}}$=-2+$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$-$\frac{n-2}{{2}^{n}}$=-$\frac{n}{{2}^{n}}$��
��Tn=-$\frac{n}{{2}^{n-1}}$��
�������ʵ���ˣ���������n��N*��ʹTn����-1��n�˺������
��-$\frac{n}{{2}^{n-1}}$����-1��n�ˣ�
nΪż��ʱ���ˣ�-$\frac{n}{{2}^{n-1}}$��
nΪ����ʱ��$�ˣ�\frac{n}{{2}^{n-1}}$��
��˲���������������ʵ���ˣ���������n��N*��ʹTn����-1��n�˺������
���� ���⿼���˵��ƹ�ϵ���Ȳ����еĶ��弰��ͨ�ʽ������λ���������ȱ����е�ǰn���ʽ���������۷���������ʽ�����ʣ�������������������������������е��⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
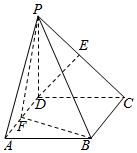 ����P-ABCD�У��ı���ABCDΪ�����Σ�PD��ƽ��ABCD��PD=DA=2��F��E�ֱ�ΪAD��PC���е㣮
����P-ABCD�У��ı���ABCDΪ�����Σ�PD��ƽ��ABCD��PD=DA=2��F��E�ֱ�ΪAD��PC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com