
已知函数 ,其中
,其中 是自然对数的底数,
是自然对数的底数, .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)当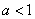 时,试确定函数
时,试确定函数 的零点个数,并说明理由.
的零点个数,并说明理由.
 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
某机构为调查中学生对“北京国际园林博览会”的了解程度,计划从某校初一年级160名学生和高一年级480名学生中抽取部分学生进行问卷调查.如果用分层抽样的方法抽取一个容量为32的样本,那么应抽取初一年级学生的人数为
A. B.
B.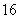 C.
C.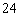 D.
D.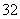
查看答案和解析>>
科目:高中数学 来源: 题型:
某中学对高二甲、乙两个同类班级进行“加强‘语文阅读理解’训练对提高‘数学应用题’得分率作用”的试验,其中甲班为试验班(加强语文阅读理解训练),乙班为对比班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用题测试的平均成绩(均取整数)如下表所示:
| 60分以下 | 61~70分 | 71~80分 | 81~90分 | 91~100分 | |
| 甲班(人数) | 3 | 6 | 11 | 18 | 12 |
| 乙班(人数) | 4 | 8 | 13 | 15 | 10 |
现规定平均成绩在80分以上(不含80分)的为优秀.
(Ⅰ)试分析估计两个班级的优秀率;
(Ⅱ)由以上统计数据填写下面2×2列联表,并问是否有75%的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助.
| 优秀人数 | 非优秀人数 | 合计 | |
| 甲班 | |||
| 乙班 | |||
| 合计 |
参考公式及数据: ,
,
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com