
分析 将直线方程代入抛物线方程,利用OM⊥ON,转化为x1x2+y1y2=0,从而可求k的值,进而可求直线l的方程.
解答 解:由题意知直线l的斜率存在,设为k,则直线l的方程为y=kx+2(k≠0),--------(1分)
与抛物线y2=2x联立,消去x得ky2-2y+4=0,-------------(3分)
△=4-16k>0⇒k<$\frac{1}{4}$(k≠0),------------(4分)
设M(x1,y1),N(x2,y2),
则y1+y2=$\frac{2}{k}$,y1•y2=$\frac{4}{k}$,-------------(5分)
y12=2x1,y22=2x2⇒x1•x2=$\frac{1}{4}$(y1•y2)2=$\frac{4}{{k}^{2}}$
∵$\overrightarrow{OM}$•$\overrightarrow{ON}$=0,∴OM⊥ON⇒kOM•kON=-1,
∴x1•x2+y1•y2=0,-------------(9分)
∴$\frac{4}{{k}^{2}}$+$\frac{4}{k}$=0,解得k=-1.-----------(10分)
所以所求直线方程为y=-x+2,即x+y-2=0.-----------(12分)
点评 本题以抛物线为载体,考查直线与抛物线的位置关系,考查学生分析解决问题的能力.


科目:高中数学 来源: 题型:解答题
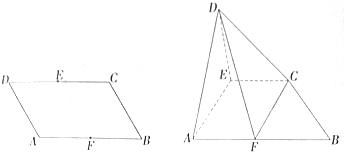
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -2 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
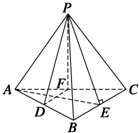
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com