
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
分析 将点(3,-$\sqrt{2}$)代入双曲线的方程,由渐近线方程可得$\frac{b}{a}$=$\frac{\sqrt{3}}{3}$,解得a,b,可得c=2,进而得到焦距2c=4.
解答 解:点(3,-$\sqrt{2}$)在双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1上,可得
$\frac{9}{{a}^{2}}$-$\frac{2}{{b}^{2}}$=1,
又渐近线方程为y=±$\frac{b}{a}$x,一条渐近线方程为y=$\frac{\sqrt{3}}{3}$x,
可得$\frac{b}{a}$=$\frac{\sqrt{3}}{3}$,
解得a=$\sqrt{3}$,b=1,
可得c=$\sqrt{{a}^{2}+{b}^{2}}$=2,
即有焦距为2c=4.
故选:D.
点评 本题考查双曲线的焦距的求法,注意运用点满足双曲线的方程和渐近线方程的运用,考查运算能力,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | 3 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
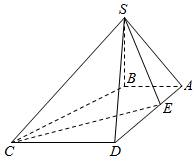 如图,在四棱锥S-ABCD中,SB⊥底面ABCD,底面ABCD为梯形,AB⊥AD,AB∥CD,AB=1,AD=3,CD=2.若点E是线段AD上的动点,则满足∠SEC=90°的点E的个数是( )
如图,在四棱锥S-ABCD中,SB⊥底面ABCD,底面ABCD为梯形,AB⊥AD,AB∥CD,AB=1,AD=3,CD=2.若点E是线段AD上的动点,则满足∠SEC=90°的点E的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e1>e2 | B. | e1<e2 | C. | e1≤e2 | D. | e1≥e2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
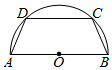 如图,半径为2的半圆有一内接梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.若双曲线以A、B为焦点,且过C、D两点,则当梯形ABCD的周长最大时,双曲线的实轴长为2$\sqrt{3}$-2.
如图,半径为2的半圆有一内接梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.若双曲线以A、B为焦点,且过C、D两点,则当梯形ABCD的周长最大时,双曲线的实轴长为2$\sqrt{3}$-2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}+\frac{y^2}{8}=1$ | B. | $\frac{x^2}{12}+\frac{y^2}{16}=1$ | C. | $\frac{x^2}{8}+\frac{y^2}{4}=1$ | D. | $\frac{x^2}{16}+\frac{y^2}{12}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 3 | C. | $\sqrt{5}$ | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com