
分析 (1)根据直线过定点求出直线方程即可;
(2)求出C的普通方程,将直线方程代入C,解出即可.
解答 解:(1)∵直线AB过定点(1,0),
故直线AB的参数方程是:$\left\{{\begin{array}{l}{x=1+tcosα}\\{y=tsinα}\end{array}}\right.(t为参数)$;
(2)∵C:$\left\{{\begin{array}{l}{x=\frac{{\sqrt{6}}}{3}cosθ}\\{y=sinθ}\end{array}}$(θ为参数),
∴曲线C:3x2+2y2=2代入得:
3(1+tcosα)2+2(tsinα)2=2,
即(cos2α+2)t2+6tcosα+1=0,
由△=36cos2α-4(cos2α+2)≥0,
解得${cos^2}α≥\frac{1}{4}即cosα≥\frac{1}{2}或cosα≤-\frac{1}{2}$,
又$α∈[{0,π})∴α∈[{0,\frac{π}{3}}]∪[{\frac{2π}{3},π})$.
点评 本题考查了求直线方程的参数式,考查参数方程和普通方程的转化以及三角函数问题,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
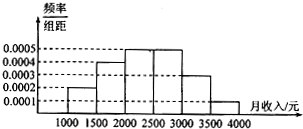 一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图所示).为了进一步分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样的方法抽出100人作进一步调查,则在[2000,2500]月收入段应抽出( )
一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图所示).为了进一步分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样的方法抽出100人作进一步调查,则在[2000,2500]月收入段应抽出( )| A. | 10人 | B. | 15人 | C. | 20人 | D. | 25人 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com