
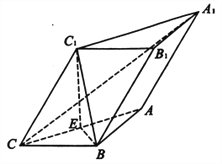
【题目】如图,在三棱柱![]() 中,平面
中,平面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,侧棱
的中点,侧棱![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析: (1)由![]() 和平面
和平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,可推得
,可推得![]() 平面
平面![]() ,进而推得
,进而推得![]() , 又
, 又![]() ,根据线面垂直的判定定理即可证得;(2)∵面
,根据线面垂直的判定定理即可证得;(2)∵面![]() 面
面![]() ,∴
,∴![]() 在面
在面![]() 上的射影
上的射影![]() 在
在![]() 上,∴
上,∴![]() 为直线
为直线![]() 与面
与面![]() 所成的角.求出CH和
所成的角.求出CH和![]() ,代入计算即可.
,代入计算即可.
试题解析:(1)证明:∵![]() ,
,![]() 为
为![]() 的中点,∴
的中点,∴![]() ,又平面
,又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,∴
,∴![]() .
.
又![]() ,
,![]() ,∴
,∴![]() 面
面![]() .
.
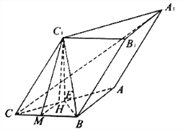
(2)∵面![]() 面
面![]() ,∴
,∴![]() 在面
在面![]() 上的射影
上的射影![]() 在
在![]() 上,∴
上,∴![]() 为直线
为直线![]() 与面
与面![]() 所成的角.过
所成的角.过![]() 作
作![]() 于
于![]() ,连
,连![]() ,
,
在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() .
.
∴在![]() 中,
中,![]() .
.
∴直线![]() 与面
与面![]() 所成的角的余弦值为
所成的角的余弦值为![]()
点睛:本题考查的是线面垂直的判定定理的应用以及求线面角,属于中档题目. 判定直线和平面垂直的方法:①定义法.②利用判定定理:一条直线和一个平面内的两条相交直线都垂直,则该直线和此平面垂直.③推论:如果在两条平行直线中,有一条垂直于一个平面,那么另一条直线也垂直这个平面.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,离心率
轴上,离心率![]() .以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为
.以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若点![]() 为椭圆
为椭圆![]() 上一点,直线
上一点,直线![]() 的方程为
的方程为![]() ,求证:直线
,求证:直线![]() 与椭圆
与椭圆![]() 有且只有一个交点.
有且只有一个交点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣[x],其中[x]表示不超过实数x的最大整数.若关于x的方程f(x)=kx+k有三个不同的实根,则实数k的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
合计 |
| 1 |

(1)求出表中![]() 及图中
及图中![]() 的值;
的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果数据x1 , x2 , …,xn的平均数是 ![]() ,方差是S2 , 则2x1+3,2x2+3,…,2xn+3的平均数和方差分别是( )
,方差是S2 , 则2x1+3,2x2+3,…,2xn+3的平均数和方差分别是( )
A.![]() 和S
和S
B.2 ![]() +3和4S2
+3和4S2
C.![]() 和S2
和S2
D.![]() 和4S2+12S+9
和4S2+12S+9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是函数y=Asin(ωx+φ)( ![]() ,
, ![]() )图
)图
像的一部分.为了得到这个函数的图像,只要将y=sin x(x∈R)的图像上所有的点( )
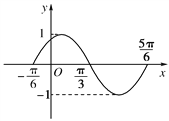
A. 向左平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() ,纵坐标不变.
,纵坐标不变.
B. 向左平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变.
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变.
C. 向左平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() ,纵坐标不变.
,纵坐标不变.
D. 向左平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变.
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com