
(本小题10分)已知圆C:x2+(y-3)2=4,一动直线l过A(-1,0)与圆C相交于P,Q两点,M是PQ的中点,l与直线m:x+3y+6=0相交于点N.
(Ⅰ)求证:当l与m垂直时,l经过圆心C;
(Ⅱ)当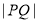 =2
=2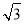 时,求直线l的方程;
时,求直线l的方程;
(Ⅲ)请问: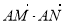 是否与直线l的倾斜角有关,若无关,请求出其值;若有关,请说明理由.
是否与直线l的倾斜角有关,若无关,请求出其值;若有关,请说明理由.
(Ⅰ)(Ⅱ)(Ⅲ)见解析
【解析】
试题分析:(Ⅰ)根据已知求出直线方程后再验证圆心满足所求直线方程;(Ⅱ)设圆的半径为r,弦心距为d,弦长为l,则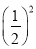 =r2-d2.利用此公式即可求得直线方程,注意斜率的讨论;(Ⅲ)有关探索性问题,一般是先假设存在满足题意的元素,经过推理论证,如果得到可以成立的结果,就可作出存在的结论;若得到与已知条件、定义、公理、定理、性质相矛盾的结果,则说明假设不存在.
=r2-d2.利用此公式即可求得直线方程,注意斜率的讨论;(Ⅲ)有关探索性问题,一般是先假设存在满足题意的元素,经过推理论证,如果得到可以成立的结果,就可作出存在的结论;若得到与已知条件、定义、公理、定理、性质相矛盾的结果,则说明假设不存在.
试题解析:(1)∵直线l与直线 垂直,且
垂直,且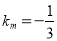
∴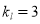 ,又
,又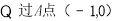
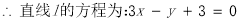
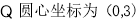
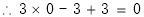 ,即圆心在直线上.
,即圆心在直线上.
 当直线l与m垂直时,直线l必过圆心C. 3分
当直线l与m垂直时,直线l必过圆心C. 3分
(2)①当直线l与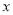 轴垂直时,易知
轴垂直时,易知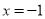 符合题意. 4分
符合题意. 4分
②当直线l与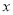 轴不垂直时,设直线l的方程为
轴不垂直时,设直线l的方程为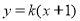 ,即
,即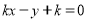 .
.
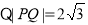 ,
,
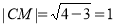 .
.
则由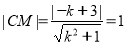 ,得
,得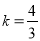 .
.
∴直线l: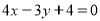 .
.
从而所求直线l的方程为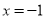 或
或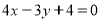 6分
6分
(3)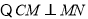 ,
,
∴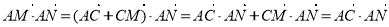

①当直线l与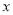 轴垂直,易得
轴垂直,易得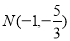 ,则
,则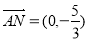
又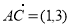 ,
,
∴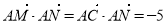 7分
7分
②当l的斜率存在时,设直线l的方程为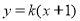 ,
,
则由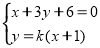 ,得
,得 . 8分
. 8分
则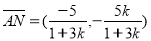 .
.
∴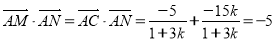 . 9分
. 9分
综上,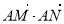 与直线l的斜率无关,且
与直线l的斜率无关,且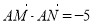 . 10分
. 10分
考点:解析几何的综合应用


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源:2014-2015学年北京市高二上学期期中练习文科数学试卷(解析版) 题型:填空题
已知平面 ,
,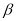 和直线
和直线  ,则满足下列条件中_______(填上所有正确的序号)
,则满足下列条件中_______(填上所有正确的序号)
能使 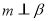 成立.
成立.
① ,②
,② ;③
;③ ;④
;④ .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市高二上学期期中练习理科数学试卷(解析版) 题型:填空题
已知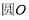 :
: ,点
,点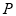 是
是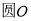 上的一动点,则
上的一动点,则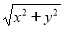 的最大值是________;
的最大值是________; 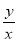 的最小值是_______.
的最小值是_______.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市高二上学期期中练习理科数学试卷(解析版) 题型:选择题
直线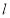 与两直线
与两直线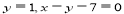 分别交于
分别交于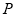 ,
,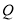 两点,线段
两点,线段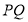 的中点是
的中点是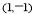 则
则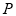 点的坐标为( )
点的坐标为( )
A.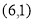 B.
B.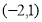 C.
C. 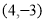 D.
D.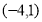
查看答案和解析>>
科目:高中数学 来源:2014-2015学年内蒙古一机一中高一上学期期中考试数学试卷(解析版) 题型:选择题
出租车按如下方法收费:起步价7元,可行3 (不含3
(不含3 );3
);3 到7
到7 (不含7
(不含7 )按
)按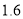 元/
元/ 计价(不足1
计价(不足1 按1
按1 计算);7
计算);7 以后按
以后按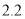 元/
元/ 计价,到目的地结算时还需付1元的燃油附加费.若从甲地坐出租车到乙地(路程
计价,到目的地结算时还需付1元的燃油附加费.若从甲地坐出租车到乙地(路程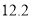
 ),需付车费(精确到1元) ( )
),需付车费(精确到1元) ( )
A、28元 B、27元 C、26元 D、25元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com