Question

5．阅读如图所示的程序框图，运行相应的程序，则输出的结果为（　　）

• A． 2
• B． 1
• C． 0
• D． -1

Answer 1

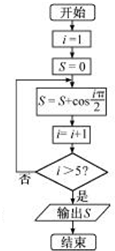
分析 模拟执行程序框图，依次写出每次循环得到的i，S的值，当i=6时满足条件i＞5，退出循环，输出S的值为0．

解答 解：模拟执行程序框图，可得
i=1，S=0
S=cos$\frac{π}{2}$，i=2
不满足条件i＞5，S=cos$\frac{π}{2}$+cosπ，i=3
不满足条件i＞5，S=cos$\frac{π}{2}$+cosπ+cos$\frac{3π}{2}$，i=4
不满足条件i＞5，S=cos$\frac{π}{2}$+cosπ+cos$\frac{3π}{2}$+cos2π，i=5
不满足条件i＞5，S=cos$\frac{π}{2}$+cosπ+cos$\frac{3π}{2}$+cos2π+cos$\frac{5π}{2}$=0-1+0+1+0=0，i=6
满足条件i＞5，退出循环，输出S的值为0，
故选：C．

点评 本题主要考查了循环结构的程序框图，正确依次写出每次循环得到的i，S的值是解题的关键，属于基础题．