
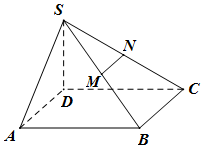
 已知四棱锥S-ABCD的底面为平行四边形,且SD⊥面ABCD,AB=2AD=2SD,∠DCB=60°,M、N分别为SB、SC中点,过MN作平面MNPQ分别与线段CD、AB相交于点P、Q.
已知四棱锥S-ABCD的底面为平行四边形,且SD⊥面ABCD,AB=2AD=2SD,∠DCB=60°,M、N分别为SB、SC中点,过MN作平面MNPQ分别与线段CD、AB相交于点P、Q.分析 (Ⅰ)利用Q是AB的中点推出图形即可.
(Ⅱ)连接PB,NB,由题可知在(Ⅰ)情况下,说明平面MNPQ与平面ABCD垂直,通过VMNCBQP=VB-MNPQ+VN-PBC,推出此多面体MNCBPQ的体积.
解答 解:(Ⅰ):如图,Q是AB的中点(若NP.PQ不是虚线,扣两分)…..(4分)
(Ⅱ)连接PB,NB,由题可知在(Ⅰ)情况下,
平面MNPQ与平面ABCD垂直,由题知AB=4,BC=PC=2,SD=2,NP=1
且SD⊥面ABCD,NP∥SD,则NP⊥面ABCD,△PCB是边长为2的等边三角形则${V_{N-PBC}}=\frac{1}{3}{S_{△PBC}}|{NP}|=\frac{1}{3}•\frac{{\sqrt{3}}}{4}•4•1=\frac{{\sqrt{3}}}{3}$…(6分)
由MN∥BC,MN⊥面SAD,面MNPQ是直角梯形,MN=NP=1,PQ=2,
连接BD交PQ于点H,在△ABD中,由余弦定理可知$BD=2\sqrt{3}$,AB2=AD2+BD2则BD⊥AD,
即BH⊥PQ,且BH⊥NP,故BH⊥面MNPQ…(9分),
${V_{B-MNPQ}}=\frac{1}{3}{S_{MNPQ}}•|{BH}|=\frac{1}{3}•\frac{{({1+2})1}}{2}•\sqrt{3}=\frac{{\sqrt{3}}}{2}$…(10分)
故VMNCBQP=VB-MNPQ+VN-PBC=$\frac{{\sqrt{3}}}{2}+\frac{{\sqrt{3}}}{3}=\frac{{5\sqrt{3}}}{6}$…..(11分)
故此多面体MNCBPQ的体积为$\frac{{5\sqrt{3}}}{6}$….(12分)
点评 本题考查直线与平面的位置关系的应用,几何体的体积的求法,考查空间想象能力以及计算能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{8}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
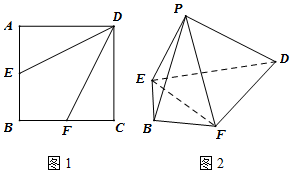 如图1,边长为4的正方形ABCD中,点E,F分别是边AB,BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点P如图2.
如图1,边长为4的正方形ABCD中,点E,F分别是边AB,BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点P如图2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
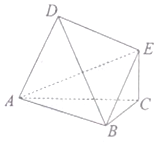 如图△ABC和△ABD均为等腰直角三角形,AD⊥BD,AC⊥BC,平面ABC⊥平面ABD,EC⊥平面ABC,EC=1,$AD=2\sqrt{2}$.
如图△ABC和△ABD均为等腰直角三角形,AD⊥BD,AC⊥BC,平面ABC⊥平面ABD,EC⊥平面ABC,EC=1,$AD=2\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | -3 | C. | -$\frac{7}{5}$ | D. | -$\frac{11}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢游泳 | 不喜欢游泳 | 合计 | |
| 男生 | 10 | ||
| 女生 | 20 | ||
| 合计 |
| p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com