
分析 求出函数的导数,得到a≠0,△>0,令f′(x),求出方程f′(x)=0的根,通过通过a的范围,得到关于a的不等式组,解出即可.
解答 解:由题意可得:f′(x)=3ax2-2x+4,
若函数f(x)=ax3-x2+4x+3恰有三个零点,
则f′(x)=0有2个不相等的实数根,
故△=4-48a>0,
令f′(x)=0,解得:x=$\frac{1±\sqrt{1-12a}}{3a}$,
a>0时,x1=$\frac{1-\sqrt{1-12a}}{3a}$<x2=$\frac{1+\sqrt{1-12a}}{3a}$,
只需$\left\{\begin{array}{l}{f{(x}_{1})>0}\\{f{(x}_{2})<0}\end{array}\right.$,解得:0<a<$\frac{14}{243}$,
a<0时,x1=$\frac{1+\sqrt{1-12a}}{3a}$<x2=$\frac{1-\sqrt{1-12a}}{3a}$,
只需$\left\{\begin{array}{l}{f{(x}_{1})>0}\\{f{(x}_{2})<0}\end{array}\right.$,解得:-2<a<0,
故答案为:(-2,0)∪(0,$\frac{14}{243}$).
点评 本题考查了函数的单调性、极值问题,考查导数的应用,是一道中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
 在几何体EFABCD中,矩形ABCD所在的平面和梯形ABEF所在的平面互相垂直,且AB∥EF,AB=2EF,设平面CBF将几何体EFABCD分成的两个锥体的体积分别为VF-ABCD,VF-CBE,求VF-ABCD:VF-CBE的值为( )
在几何体EFABCD中,矩形ABCD所在的平面和梯形ABEF所在的平面互相垂直,且AB∥EF,AB=2EF,设平面CBF将几何体EFABCD分成的两个锥体的体积分别为VF-ABCD,VF-CBE,求VF-ABCD:VF-CBE的值为( )| A. | 2:1 | B. | 3:1 | C. | 4:1 | D. | 5:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f($\frac{5}{2}$)<f(1)<f($\frac{7}{2}$) | B. | f(1)<f($\frac{7}{2}$)<f($\frac{5}{2}$) | C. | f($\frac{7}{2}$)<f(1)<f($\frac{5}{2}$) | D. | f($\frac{7}{2}$)<f($\frac{5}{2}$)<f(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
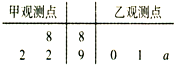 如图,茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数(AQI).乙观测点记录中有一个数字模糊无法确认,已知该数是0,1,…,9中随机的一个数,并在图中以a表示.
如图,茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数(AQI).乙观测点记录中有一个数字模糊无法确认,已知该数是0,1,…,9中随机的一个数,并在图中以a表示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 1 | 2 | 3 | 4 |
| y | 0.4 | 0.9 | 1.1 | 1.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com