
分析 根据sinα,cosα的符号,对角α分五类进行讨论,由直线、圆、椭圆和双曲线的标准方程判断对应曲线的具体类型.
解答 解:当α≠90°时,∵x2sinα+y2cosα=1,∴$\frac{{x}^{2}}{\frac{1}{sinα}}+\frac{{y}^{2}}{\frac{1}{cosα}}=1$.
(1)当0°<α<45°时,0<sinα<cosα,曲线是焦点在X轴上的椭圆;(3分)
(2)当α=45°时,$\frac{\sqrt{2}}{2}$,曲线是圆;(2分)
(3)当45°<α<90°时,sinα>cosα>0,曲线是焦点在Y轴上的椭圆;(3分)
(4)当α=90°时,方程为x=±1,曲线是两条直线;(2分)
(5)90°<α<180°时,sinα>0,cosα<0,曲线是焦点在X轴上的双曲线.(4分)
点评 本题考查了方程含有参数时讨论表示的曲线问题,需要根据系数的符号进行分类讨论,分别再由圆、椭圆和双曲线的标准方程判断对应曲线的具体形状,考查了分类讨论思想.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设函数f(x)是定义在区间(-∞,+∞)上以2为周期的函数,记Ik=(2k-1,2k+1](k∈Z).已知当x∈I0时,f(x)=x2,如图.
设函数f(x)是定义在区间(-∞,+∞)上以2为周期的函数,记Ik=(2k-1,2k+1](k∈Z).已知当x∈I0时,f(x)=x2,如图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
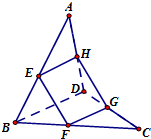 如图,E,F,G,H分别是空间四边形ABCD四边的中点.
如图,E,F,G,H分别是空间四边形ABCD四边的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 不是充分条件,也不是必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com