
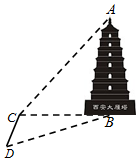
 如图,某数学兴趣小组为了测量西安大雁塔高AB,选取与塔底B在同一水平面
如图,某数学兴趣小组为了测量西安大雁塔高AB,选取与塔底B在同一水平面分析 先在△BCD中利用正弦定理计算BC,再在△ABC中求出AB.
解答 解:在△BCD中,∠CBD=180°-45°-105°=30°,
由正弦定理得$\frac{BC}{sin∠BDC}=\frac{CD}{sin∠CBD}$,即$\frac{BC}{\frac{\sqrt{2}}{2}}=\frac{26.4}{\frac{1}{2}}$,解得BC=26.4×$\sqrt{2}$,
在Rt△ABC中,∵tan∠ACB=$\frac{AB}{BC}$=$\sqrt{3}$,
∴AB=$\sqrt{3}$BC=26.4×$\sqrt{6}$≈64.68.
故答案为:64.68.
点评 本题考查了解三角形的实际应用,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [5,6] | B. | [2,5] | C. | [2,5) | D. | (-∞,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD为梯形,CD∥AB,AB=2CD,AC交BD于O,锐角△PAD所在平面⊥底面ABCD,PA⊥BD,点Q在侧棱PC上,且PQ=2QC.
如图,在四棱锥P-ABCD中,底面ABCD为梯形,CD∥AB,AB=2CD,AC交BD于O,锐角△PAD所在平面⊥底面ABCD,PA⊥BD,点Q在侧棱PC上,且PQ=2QC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com